
| A. | y=ex | B. | y=lnx | C. | y=x2 | D. | y=$\frac{x-1}{x+1}$ |
分析 由自變量與對應的函數值不相等判斷A,B,D不合題意;舉例說明C正確.
解答 解:函數y=ex在定義域內為增函數,而ex>x恒成立,∴不存在實數m使得定義域和值域都是(m,+∞);
函數y=lnx在定義域內為增函數,而x>lnx恒成立,∴不存在實數m使得定義域和值域都是(m,+∞);
當m=0時,y=x2的定義域和值域都是(m,+∞),符合題意;
對于$y=\frac{x-1}{x+1}$,由$\frac{x-1}{x+1}=x$,得x2=-1,方程無解,∴不存在實數m使得定義域和值域都是(m,+∞).
故選:C.
點評 本題考查函數的定義域及其求法,考查了函數的值域,體現了數學轉化思想方法,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 有且僅有一條 | B. | 有且僅有兩條 | C. | 有無窮多條 | D. | 不存在 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x0∈R,lnx0<0 | B. | ?x∈(-∞,0),ex>0 | ||
| C. | ?x>0,5x>3x | D. | ?x0∈(0,+∞),2<sinx0+cosx0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
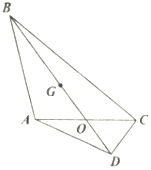 如圖,在平面四邊形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如圖,在平面四邊形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com