
分析 (1)根據平面向量的數量積公式和三角恒等變換化簡f(x),根據正弦函數的性質求出f(x)的零點;
(2)根據f(A)=1求出A,利用正弦定理和正弦函數的性質得出$\frac{b+c}{a}$的范圍.
解答 解:(1)由條件可知:$\overrightarrow a•\overrightarrow b=cosx•sin(x-\frac{π}{6})+sinx•cos(x-\frac{π}{6})=sin(2x-\frac{π}{6})$,
∴$f(x)=\overrightarrow a•\overrightarrow b=sin(2x-\frac{π}{6})$.
令$sin(2x-\frac{π}{6})=0$,得2x-$\frac{π}{6}$=kπ,∴$x=\frac{kπ}{2}+\frac{π}{12}$,k∈Z.
∴f(x)的零點為$\frac{π}{12}$+$\frac{kπ}{2}$,k∈Z.
(2)由正弦定理得$\frac{b+c}{a}=\frac{sinB+sinC}{sinA}$
由(1)f(A)=sin(2A-$\frac{π}{6}$)=1,
∴$2A-\frac{π}{6}=2kπ+\frac{π}{2}$,k∈Z,又A∈(0,π),∴$A=\frac{π}{3}$,
∴$C=\frac{2π}{3}-B$,
∴$\frac{b+c}{a}=\frac{{sinB+sin(\frac{2π}{3}-B)}}{sinA}=\frac{{\frac{3}{2}sinB+\frac{{\sqrt{3}}}{2}cosB}}{sinA}=\frac{{\sqrt{3}sin(B+\frac{π}{6})}}{sinA}=2sin(B+\frac{π}{6})$,
∵$0<B<\frac{2π}{3}$,∴$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,∴$\frac{1}{2}<sin(B+\frac{π}{6})≤1$.
∴$1<\frac{b+c}{a}≤2$.
點評 本題考查了平面向量的數量積運算,三角恒等變換,正弦定理,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
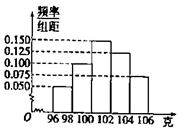 某工廠對一批產品進行了抽樣檢測,如圖是根據抽樣檢測后的產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),[100,102),[102,104),(104,106],已知樣本中產品凈重小于100克的個數是36,則樣本中凈重大于或等于98克并且小于104克的產品的個數是( )
某工廠對一批產品進行了抽樣檢測,如圖是根據抽樣檢測后的產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),[100,102),[102,104),(104,106],已知樣本中產品凈重小于100克的個數是36,則樣本中凈重大于或等于98克并且小于104克的產品的個數是( )| A. | 90 | B. | 75 | C. | 60 | D. | 45 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
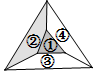 《數學萬花筒》第7頁中談到了著名的“四色定理”.問題起源于1852年的倫敦大學學院畢業生弗朗西斯•加斯里.他給自己的弟弟弗萊德里克寫的信中提到:“可以使用四種(或更少)顏色為平面上畫出的每張地圖著色,使任何相鄰的兩個地區的邊界線具有不同的顏色嗎?”回答他這個問題用了124年,但簡單的圖形我們能用逐一列舉的方法解決.若用紅、黃、藍、綠四種顏色給右邊的地圖著色,假定區域①已著紅色,區域②已著黃色,則剩余的區域③④共有2種著色方法.
《數學萬花筒》第7頁中談到了著名的“四色定理”.問題起源于1852年的倫敦大學學院畢業生弗朗西斯•加斯里.他給自己的弟弟弗萊德里克寫的信中提到:“可以使用四種(或更少)顏色為平面上畫出的每張地圖著色,使任何相鄰的兩個地區的邊界線具有不同的顏色嗎?”回答他這個問題用了124年,但簡單的圖形我們能用逐一列舉的方法解決.若用紅、黃、藍、綠四種顏色給右邊的地圖著色,假定區域①已著紅色,區域②已著黃色,則剩余的區域③④共有2種著色方法.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com