
分析 ①利用正弦定理求出AC的值,再利用平面向量的數量積計算f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$;
②由①化簡f(x),利用θ的取值范圍,求出正弦函數的取值范圍即可.
解答 解:①如圖所示,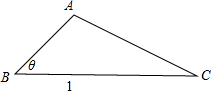
△ABC中,BC=1,A=120°,∠B=θ,
由正弦定理得,$\frac{AC}{sinθ}$=$\frac{BC}{sinA}$=$\frac{1}{sin120°}$=$\frac{2}{\sqrt{3}}$
∴AC=$\frac{2sinθ}{\sqrt{3}}$
∴f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$
=1×$\frac{2sinθ}{\sqrt{3}}$×cos(180°-120°-θ)
=$\frac{2sinθ}{\sqrt{3}}$×(cos60°cosθ+sin60°sinθ)
=$\frac{1}{\sqrt{3}}$sinθcosθ+sin2θ
=$\frac{1}{2\sqrt{3}}$sin2θ-$\frac{1}{2}$cos2θ+$\frac{1}{2}$
=$\frac{1}{\sqrt{3}}$($\frac{1}{2}$sin2θ-$\frac{\sqrt{3}}{2}$cos2θ)+$\frac{1}{2}$
=$\frac{\sqrt{3}}{3}$sin(2θ-60°)+$\frac{1}{2}$,其中θ∈(0°,60°);
②由①知,θ∈(0°,60°),
∴2θ∈(0°,120°),
∴2θ-60°∈(-60°,60°),
∴sin(2θ-60°)∈(-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$)
∴$\frac{\sqrt{3}}{3}$sin(2θ-60°)+$\frac{1}{2}$∈(0,1);
即f(θ)的值域是(0,1).
點評 本題考查了平面向量的數量積運算與三角函數的圖象與性質的應用問題,是綜合題.


科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
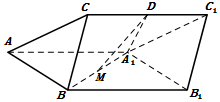 如圖,三棱柱ABC-A1B1C1中,側面ABB1A1為菱形且$∠BA{A_1}={60^o}$,D,M分別為CC1和A1B的中點,A1D⊥CC1,AA1=A1D=2,BC=1.
如圖,三棱柱ABC-A1B1C1中,側面ABB1A1為菱形且$∠BA{A_1}={60^o}$,D,M分別為CC1和A1B的中點,A1D⊥CC1,AA1=A1D=2,BC=1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
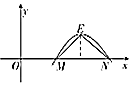 已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函數f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的導函數的部分圖象如圖所示,E是最高點,且△MNE是邊長為1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com