
分析 (I)化簡函數f(x),求出f(x)得最大值的x的取值集合;
(II)求函數g(x)的導數,利用函數單調性和導數之間的關系解g(x)的單調遞減區間.
解答 解:( I)∵$f(x)=cosx-\sqrt{3}sinx=2cos(x+\frac{π}{3})$,
當$x+\frac{π}{3}=2kπ$,即$x=2kπ-\frac{π}{3}$時,f(x)取得最大值2.
所以使得f(x)取得最大值的x的取值集合為$\{x|x=2kπ-\frac{π}{3},k∈Z\}$.
( II)∵$g(x)=x+cosx-\sqrt{3}sinx$,
∴$g'(x)=1-sinx-\sqrt{3}cosx$.
令g'(x)<0,得$1-sinx-\sqrt{3}cosx<0$,
∴$sinx+\sqrt{3}cosx>1$,
∴$2sin(x+\frac{π}{3})>1$,
∴$sin(x+\frac{π}{3})>\frac{1}{2}$,
∴$2kπ+\frac{π}{6}<x+\frac{π}{3}<kπ+\frac{5π}{6}$,k∈Z,
∴$2kπ-\frac{π}{6}<x<2kπ+\frac{π}{2}$,k∈Z,
∴g(x)的單調遞減區間為$[2kπ-\frac{π}{6},2kπ+\frac{π}{2}]$,k∈Z.
點評 本題主要考查函數單調性和單調區間的求解,利用正弦函數的單調性的性質或者導數法時解決本題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -a>-b | B. | a+c>b+c | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | (-a)2>(-b)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
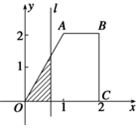 如圖,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直線l:x=t截此梯形所得位于l左方圖形面積為S,則函數S=f(t)的圖象大致為圖中的( )
如圖,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直線l:x=t截此梯形所得位于l左方圖形面積為S,則函數S=f(t)的圖象大致為圖中的( )| A. |  | B. | 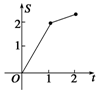 | C. |  | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com