
分析 (1)當a=2時,函數$f(x)=x+\frac{2}{x}+2,x∈[2,+∞)$.f(x)在[2,+∞)上是增函數,所以最小值為f(2).
(2)在區間[1,+∞)上,$xf(x)={x^2}+2x+a>\frac{2a+6}{|a|}$恒成立.令g(x)=x2+2x+a,x≥1,而函數g(x)在[1,+∞)上是增函數,則g(x)的最小值為gmin(x)=3+a.
解答 解:(1)當a=2時,函數$f(x)=x+\frac{2}{x}+2,x∈[2,+∞)$.
f(x)在[2,+∞)上是增函數.
所以f(x)在區間[2,+∞)上的最小值為f(2)=5.
(2)在區間[1,+∞)上,$xf(x)={x^2}+2x+a>\frac{2a+6}{|a|}$恒成立.
令g(x)=x2+2x+a,x≥1,而函數g(x)在[1,+∞)上是增函數,
則g(x)的最小值為gmin(x)=3+a,
所以當且僅當$3+a>\frac{2a+6}{|a|}$時恒成立,所以a>2或-3<a<-2.
點評 本題主要考查了導數研究函數單調性,以及導數在恒成立問題中的應用,屬中等題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
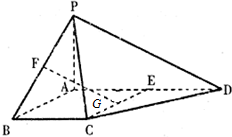 四棱錐P-ABCD中,PA⊥平面ABCD,E為AD的中點,四邊形ABCE為菱形,∠BAD=120°,G、F分別是線段CE,PB上的動點,且滿足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$
四棱錐P-ABCD中,PA⊥平面ABCD,E為AD的中點,四邊形ABCE為菱形,∠BAD=120°,G、F分別是線段CE,PB上的動點,且滿足$\frac{PF}{PB}=\frac{CG}{CE}=λ∈(0,1)$查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com