Question

6．在△ABC中，BC=2，AC=$\sqrt{2}$，AB=$\sqrt{3}$+1．設△ABC的外心為O，若$\overrightarrow{AC}$=m$\overrightarrow{AO}$+n$\overrightarrow{AB}$，則m+n=-1．

Answer 1

分析 設AB，AC中點分別為M，N，利用向量的三角形法則和三角形的外心的性質即可得出答案．

解答 解：設AB，AC中點分別為M，N，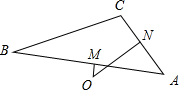

則$\overrightarrow{OM}$=$\overrightarrow{AM}$-$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{m}$（$\overrightarrow{AC}$-n$\overrightarrow{AB}$）=（$\frac{1}{2}+\frac{n}{m}$）$\overrightarrow{AB}$-$\frac{1}{m}$$\overrightarrow{AC}$，
$\overrightarrow{ON}$=$\overrightarrow{AN}$-$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\frac{1}{m}$（$\overrightarrow{AC}$-n$\overrightarrow{AB}$）=$\frac{n}{m}$$\overrightarrow{AB}$+（$\frac{1}{2}-$$\frac{1}{m}$）$\overrightarrow{AC}$，
由外心O的定義知，$\overrightarrow{OM}$⊥$\overrightarrow{AB}$，$\overrightarrow{ON}$⊥$\overrightarrow{AC}$，
因此，$\overrightarrow{OM}$•$\overrightarrow{AB}$=0，$\overrightarrow{ON}$•$\overrightarrow{AC}$=0，
∴[（$\frac{1}{2}+\frac{n}{m}$）$\overrightarrow{AB}$-$\frac{1}{m}$$\overrightarrow{AC}$]•$\overrightarrow{AB}$=0，[$\frac{n}{m}$$\overrightarrow{AB}$+（$\frac{1}{2}-$$\frac{1}{m}$）$\overrightarrow{AC}$]•$\overrightarrow{AC}$=0，
即（$\frac{1}{2}+\frac{n}{m}$）$\overrightarrow{AB}$²-$\frac{1}{m}$$\overrightarrow{AC}$•$\overrightarrow{AB}$=0…①，$\frac{n}{m}$$\overrightarrow{AB}$•$\overrightarrow{AC}$+（$\frac{1}{2}-$$\frac{1}{m}$）$\overrightarrow{AC}$²=0…②，
∵$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$，
∴$\overrightarrow{BC}$²=$\overrightarrow{AC}$²-2$\overrightarrow{AB}$•$\overrightarrow{AC}$+$\overrightarrow{AB}$²，
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{1}{2}$（$\overrightarrow{AC}$²+$\overrightarrow{AB}$²-$\overrightarrow{BC}$²）=1+$\sqrt{3}$…③，
將③代入①②得：$\left\{\begin{array}{l}（\frac{1}{2}+\frac{n}{m}）（4+2\sqrt{3}）-\frac{1}{m}（1+\sqrt{3}）=0\\ \frac{n}{m}（1+\sqrt{3}）+2（\frac{1}{2}-\frac{1}{m}）=0\end{array}\right.$，
解得：$\left\{\begin{array}{l}m=-1-\sqrt{3}\\ n=\sqrt{3}\end{array}\right.$
∴m+n=-1，
故答案為：-1

點評 本題以向量在平面幾何中的應用為載體，考查了向量的三角形法則和三角形的外心的性質，屬于難題．