Question

11．如圖，在三棱柱ABC-A₁B₁C₁中，AB⊥BC，AB₁⊥平面ABC，且AB=BC=AB₁=2．
（Ⅰ）證明：平面C₁CBB₁⊥平面A₁ABB₁
（Ⅱ）若點P為A₁C₁的中點，求直線BP與平面A₁ACC₁所成角的正弦值．

Answer 1

分析 （Ⅰ）B₁A⊥平面ABC，則B₁A⊥BC，AB⊥BC，BC⊥平面A₁ABB₁，BC?平面C₁CBB₁，平面C₁CBB₁⊥平面A₁ABB₁；
（Ⅱ）分別以$\overrightarrow{BC}，\overrightarrow{BA}，\overrightarrow{BM}$為x，y，z軸的非負向量建立空間直角坐標系B-xyz，求得$\overrightarrow{BP}$=（1，3，2）和平面A₁ACC₁法向量，直線BP與平面A₁ACC₁所成角的余弦值為丨cos＜$\overrightarrow{n}$，$\overrightarrow{BP}$＞丨=丨$\frac{1+3-2}{\sqrt{3}×\sqrt{14}}$丨=$\frac{\sqrt{42}}{21}$，根據(jù)同角三角形函數(shù)的基本關(guān)系，即可求得直線BP與平面A₁ACC₁所成角的正弦值．

解答 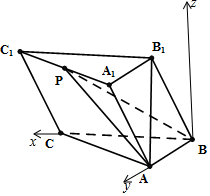解：（Ⅰ）證明：∵B₁A⊥平面ABC，
∴B₁A⊥BC…（1分），
又∵AB⊥BC，AB∩BC=B，
∴BC⊥平面A₁ABB₁，…（3分），
又∵BC?平面C₁CBB₁，
∴平面C₁CBB₁⊥平面A₁ABB₁…（4分）
（Ⅱ）過B點作BM⊥平面ABC，則BM⊥BA，BM⊥BC，分別以$\overrightarrow{BC}，\overrightarrow{BA}，\overrightarrow{BM}$為x，y，z軸的非負向量建立空間直角坐標系B-xyz，…（5分），
則B（0，0，0），B₁（0，2，2），
∵$\overrightarrow{A{A}_{1}}$=$\overrightarrow{B{B}_{1}}$=$\overrightarrow{C{C}_{1}}$=（0，2，2），
∴A₁（0，4，2），C₁（2，2，2），P（1，3，2），
∴$\overrightarrow{AC}$=（2，-2，0），$\overrightarrow{BP}$=（1，3，2），
設(shè)$\overrightarrow{n}$=（x，y，z）為平面A₁ACC₁的一個法向量，
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=0}\\{\overrightarrow{n}•\overrightarrow{A{A}_{1}}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{2x-2y=0}\\{2y+2z=0}\end{array}\right.$，取x=1，解得：y=1，z=-1，
∴$\overrightarrow{n}$=（1，1，-1），
故直線BP與平面A₁ACC₁所成角的余弦值為丨cos＜$\overrightarrow{n}$，$\overrightarrow{BP}$＞丨=丨$\frac{1+3-2}{\sqrt{3}×\sqrt{14}}$丨=$\frac{\sqrt{42}}{21}$，
sin＜$\overrightarrow{n}$，$\overrightarrow{BP}$＞=$\sqrt{1-（\frac{\sqrt{42}}{21}）^{2}}$=$\frac{\sqrt{399}}{21}$．…（12分）

點評 本題考查的知識點是用空間向量求直線與平面的夾角，考查立體幾何與向量的綜合應(yīng)用，考查平面法向量的求法，考查計算能力，屬于中檔題．