
分析 (1)由橢圓的離心率公式,求得a=2c,b2=a2-c2=2c2,由函數的對稱性可知:ME的直線方程為y=x+1,代入橢圓方程,由△=0,即可求得c值,即可求得a和b,求得橢圓方程;
(2)設l的方程,代入橢圓方程,利用韋達定理及向量數量積的坐標運算,即可求得t的范圍.
解答 解:(1)由題意的橢圓的離心率e=$\frac{c}{a}$=$\frac{1}{2}$,則a=2c,b2=a2-c2=2c2,
由橢圓的對稱性,不妨設在x軸上方的切點為M,x軸下方的切點為N,則kME=1,ME的直線方程為y=x+1,
所以$\left\{{\begin{array}{l}{y=x+\sqrt{7}}\\{\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1}\end{array}}\right.$,整理得:7x2+8$\sqrt{7}$x+28-12c2=0
△=(8$\sqrt{7}$)2-4×7×(28-12c2)=0,解得:c=1,
∴∴橢圓方程為$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)設l的方程為x=my+t,A(x1,y1),B(x2,y2),
則$\left\{{\begin{array}{l}{my+t=x}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,(3m2+4)y2+6mty+3t2-12=0,
${y_1}+{y_2}=\frac{-6mt}{{3{m^2}+4}},{y_1}{y_2}=\frac{{3{t^2}-12}}{{3{m^2}+4}}$$\overrightarrow{FA}=({x_1}-1,{y_1})$,
$\overrightarrow{FB}=({x_2}-1,{y_2})$,$\overrightarrow{FA}$•$\overrightarrow{FB}$=(x2-1)(x1-1)+y1y2=x1x2-(x1+x2)+1+y1y2
=$({m^2}+1){y_1}{y_2}+(mt-m)({y_1}+{y_2})+{t^2}-2t+1=0$,
∴7t2-8t-8=9m2有解,
∴7t2-8t-8≥0,則$t≥\frac{{4+6\sqrt{2}}}{7}$或$t≤\frac{{4-6\sqrt{2}}}{7}$.
∴t的范圍(-∞,$\frac{4-6\sqrt{2}}{7}$]∪[$\frac{4+6\sqrt{2}}{7}$,+∞).
點評 本題考查橢圓的標準方程,直線與橢圓的位置關系,考查韋達定理,向量數量積的坐標運算,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
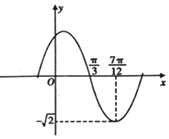 函數f(x)=Asin(ωx+φ),(A,ω,φ是常數,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分圖象如圖所示,則y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范圍是( )
函數f(x)=Asin(ωx+φ),(A,ω,φ是常數,A>0,ω>0,|φ|≤$\frac{π}{2}$)的部分圖象如圖所示,則y=f(x)在x∈[-$\frac{π}{4}$,$\frac{π}{2}$]上的取值范圍是( )| A. | [-$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | B. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] | C. | [-$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] | D. | [$\frac{\sqrt{6}}{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 上春晚次數x(單位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉絲數量y(單位:萬人) | 10 | 20 | 40 | 80 | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | -2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com