Question

10．設(shè)x，y滿足約束條件$\left\{\begin{array}{l}3x-y-2≤0\\ x-y≥0\\ x≥0，y≥0\end{array}\right.$，若目標(biāo)函數(shù)z=ax+by（a＞0，b＞0）的最大值為2，則$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$的最小值為（　　）

• A． 2
• B． $\frac{8}{3}$
• C． $\frac{25}{6}$
• D． 4

Answer 1

分析 作出不等式組對(duì)應(yīng)的平面區(qū)域，利用目標(biāo)函數(shù)取得最大值，確定a，b的關(guān)系，利用基本不等式求$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$的最小值．

解答 解：作出不等式組對(duì)應(yīng)的平面區(qū)域如圖：（陰影部分OAC），
由z=ax+by（a＞0，b＞0），則y=-$\frac{a}{b}$x+$\frac{z}{b}$，
平移直線y=-$\frac{a}{b}$x+$\frac{z}{b}$，由圖象可知當(dāng)直線y=-$\frac{a}{b}$x+$\frac{z}{b}$經(jīng)過(guò)點(diǎn)是，直線的截距最大，此時(shí)z最大為2．
由$\left\{\begin{array}{l}{3x-y-2=0}\\{x-y=0}\end{array}\right.$，解得C（1，1），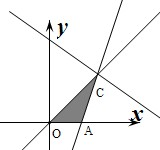
代入目標(biāo)函數(shù)z=ax+by得a+b=2．
∴$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$=$\frac{1}{2}$（$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$）（a+b）=$\frac{1}{2}$（1+$\frac{a}{b}$+$\frac{b}{a}$+1）=1+$\frac{1}{2}$（$\frac{a}{b}$+$\frac{b}{a}$）≥1+$\sqrt{\frac{a}{b}•\frac{b}{a}}$=2，
當(dāng)且僅當(dāng)$\frac{a}{b}$=$\frac{b}{a}$即a=b=1時(shí)取等號(hào)，
∴$\frac{1}{a}+\frac{1}{{{b^{\;}}}}$的最小值為2．
故選：A．

點(diǎn)評(píng) 本題主要考查線性規(guī)劃的應(yīng)用，利用數(shù)形結(jié)合是解決此類問(wèn)題的基本方法，利用基本不等式的性質(zhì)可求表達(dá)式的最小值．