Question

18．已知點P為棱長等于2的正方體ABCD-A₁B₁C₁D₁內部一動點，且$|{\overrightarrow{PA}}|=2$，則$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值達到最小時，$\overrightarrow{P{C_1}}$與$\overrightarrow{P{D_1}}$夾角大小為90°．

Answer 1

分析 以D為原點，DA、DC、DD₁為x，y，z軸建立空間直角坐標系，
利用坐標表示$|{\overrightarrow{PA}}|=2$，則點P的軌跡是以A為球心，2為半徑的球面一部分；
計算$\overrightarrow{P{C}_{1}}$•$\overrightarrow{P{D}_{1}}$=x²+（y-1）²+（z-2）²-1，
它表示點P到點M（0，1，2）的距離的平方再減去1；
由圖形知P為AM與所在的球面交點時，$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值最小，
求出點P的坐標，利用數量積求出$\overrightarrow{P{C_1}}$與$\overrightarrow{P{D_1}}$的夾角．

解答 解：以D為原點，DA、DC、DD₁為x，y，z軸建立空間直角坐標系，
如圖所示；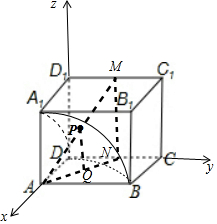
由棱長為2，得A（2，0，0），C₁（0，2，2），D₁（0，0，2），
設P（x，y，z），
由且$|{\overrightarrow{PA}}|=2$，則（x-2）²+y²+z²=4①，
點P的軌跡表示以A為球心，以2為半徑的球面的一部分；
又$\overrightarrow{P{C}_{1}}$=（-x，2-y，2-z），$\overrightarrow{P{D}_{1}}$=（-x，-y，2-z），
∴$\overrightarrow{P{C}_{1}}$•$\overrightarrow{P{D}_{1}}$=x²-2y+y²+（z-2）²
=x²+（y-1）²+（z-2）²-1②，
它表示點P到點M（0，1，2）的距離的平方再減去1；
由圖形知，當P為AM與①所在的球面交點時，$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$的值最小，
此時AM=3，AP=2；
∴x=$\frac{2}{3}$，y=$\frac{2}{3}$，z=$\frac{4}{3}$；
∴$\overrightarrow{P{C_1}}•\overrightarrow{P{D_1}}$=${（\frac{2}{3}）}^{2}$+${（\frac{2}{3}-1）}^{2}$+${（\frac{4}{3}-1）}^{2}$-1=0，
∴$\overrightarrow{P{C_1}}$與$\overrightarrow{P{D_1}}$夾角為90°．
故答案為：90°．

點評 本題考查了空間直角坐標系與空間向量的應用問題，是較難的題目．