
分析 (1)根據根與系數的關系即可得出x1+x2=2、x1•x2=-3,將$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$變形為$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$,代入數據即可得出結論;
(2)由x1+x2=2、x1•x2=-3可得出(-x1)+(-x2)=-(x1+x2)=-2、(-x1)•(-x2)=x1•x2=-3,結合根與系數的關系即可得出當a為1時,以-x1和-x2為兩根的一元二次方程,此題得解.
解答 解:(1)∵x1,x2是方程x2-2x-3=0的兩個根,
∴x1+x2=2,x1•x2=-3,
∴$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}•{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$=-$\frac{10}{3}$.
(2)∵x1+x2=2,x1•x2=-3,
∴(-x1)+(-x2)=-(x1+x2)=-2,(-x1)•(-x2)=x1•x2=-3,
∴當a=1時,-x1和-x2是方程x2+2x-3=0的解,
即新方程為x2+2x-3=0.
點評 本題考查了根與系數的關系,解題的關鍵是:(1)根據根與系數的關系找出x1+x2=2、x1•x2=-3;(2)利用根與系數的關系找出當a=1時的一元二次方程,


科目:初中數學 來源: 題型:解答題
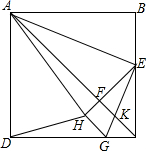 如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.
如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
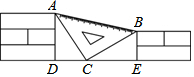 課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.
課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
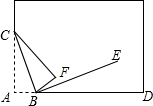 如圖,將長方形紙片的一角折疊,使頂點A落在F處,折痕為BC.
如圖,將長方形紙片的一角折疊,使頂點A落在F處,折痕為BC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
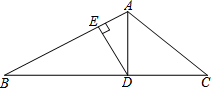 如圖,AD是△ABC中∠BAC的角平分線,DE⊥AB于點E,AB=8,DE=4,AC=6,則△ACD的面積為( )
如圖,AD是△ABC中∠BAC的角平分線,DE⊥AB于點E,AB=8,DE=4,AC=6,則△ACD的面積為( )| A. | 8 | B. | 10 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{5}{2}$ x2y與-$\frac{3}{2}$ xy3 | B. | -8a2b與5a2c | C. | $\frac{1}{4}$ pq與-$\frac{5}{2}$ qp | D. | 19abc與-28ab |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com