
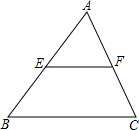
 如圖,△ABC中,E、F分別是AB、AC的中點,若△AEF的面積為1,則四邊形EBCF的面積為3.
如圖,△ABC中,E、F分別是AB、AC的中點,若△AEF的面積為1,則四邊形EBCF的面積為3. 分析 根據三角形中位線定理得到EF∥BC,EF=$\frac{1}{2}$BC,得到△AEF∽△ABC,根據相似三角形的面積比等于相似比的平方計算即可.
解答 解:∵E、F分別是AB、AC的中點,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△AEF∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=($\frac{1}{2}$)2,
∵△AEF的面積為1,
∴△ABC的面積為4,
∴四邊形EBCF的面積為4-1=3,
故答案為:3.
點評 本題考查的是相似三角形的判定和性質、三角形中位線定理的應用,掌握相似三角形的判定定理和性質定理是解題的關鍵.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 所有的矩形都相似 | |
| B. | 所有的直角三角形都相似 | |
| C. | 有一個角是50°的所有等腰三角形都相似 | |
| D. | 有一個角是100°的所有等腰三角形都相似 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{a+b}{m+n}$ | B. | $\frac{1}{2}$($\frac{a}{m}$+$\frac{b}{n}$) | C. | $\frac{am+bn}{m+n}$ | D. | $\frac{1}{2}$(am+bn) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
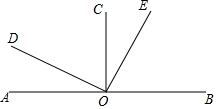 如圖,己知直線AB上一點O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.
如圖,己知直線AB上一點O,OC⊥AB,OD⊥OE,若∠COE=$\frac{1}{5}$∠BOD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com