
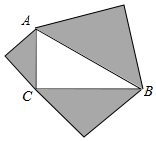
 如圖,分別以Rt△ABC的三邊為斜邊向外作等腰直角三角形,若斜邊AB=4,則圖中陰影部分的面積為( )
如圖,分別以Rt△ABC的三邊為斜邊向外作等腰直角三角形,若斜邊AB=4,則圖中陰影部分的面積為( )| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
分析 根據(jù)勾股定理和等腰直角三角形的面積公式,可以證明:以直角三角形的兩條直角邊為斜邊的等腰直角三角形的面積和等于以斜邊為斜邊的等腰直角三角形的面積.則陰影部分的面積即為以斜邊為斜邊的等腰直角三角形的面積的2倍.
解答 解:在Rt△AHC中,AC2=AH2+HC2,AH=HC,
∴AC2=2AH2,
∴HC=AH=$\frac{AC}{\sqrt{2}}$,
同理;CF=BF=$\frac{BC}{\sqrt{2}}$,BE=AE=$\frac{AB}{\sqrt{2}}$,
在Rt△ABC中,AB2=AC2+BC2,AB=4,
S陰影=S△AHC+S△BFC+S△AEB=$\frac{1}{2}$HC•AH+$\frac{1}{2}$CF•BF+$\frac{1}{2}$AE•BE,
=$\frac{1}{2}$×($\frac{AC}{\sqrt{2}}$)2+$\frac{1}{2}$×($\frac{BC}{\sqrt{2}}$)2+$\frac{1}{2}$($\frac{AB}{\sqrt{2}}$)2=$\frac{1}{4}$(AC2+BC2+AB2)
=$\frac{1}{4}$(AB2+AB2)
=$\frac{1}{4}$×2AB2
=$\frac{1}{2}$AB2
=$\frac{1}{2}$×42
=8.
故選B.
點(diǎn)評(píng) 本題考查了勾股定理的知識(shí),難度適中,解題關(guān)鍵是運(yùn)用勾股定理證明三個(gè)等腰直角三角形的面積之間的關(guān)系.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | -$\frac{1}{4}$ | B. | 4 | C. | -4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com