
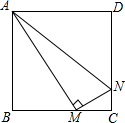
 如圖,正方形ABCD的邊長為1cm,M、N分別是BC、CD上兩個動點,且始終保持AM⊥MN,則△ADN的最小面積為$\frac{3}{8}$cm2.
如圖,正方形ABCD的邊長為1cm,M、N分別是BC、CD上兩個動點,且始終保持AM⊥MN,則△ADN的最小面積為$\frac{3}{8}$cm2. 分析 設BM=xcm,則MC=(1-x)cm,當AM⊥MN時,利用互余關系可證△ABM∽△MCN,利用相似比求CN,根據三角形的面積公式表示出△ADN的面積,用二次函數的性質求面積的最小值.
解答 解:設BM=xcm,則MC=(1-x)cm,
∵∠AMN=90°,
∴∠AMB+∠NMC=90°,∠NMC+∠MNC=90°,
∴∠AMB=∠MNC,
又∵∠B=∠C,
∴△ABM∽△MCN,則$\frac{AB}{MC}$=$\frac{BM}{CN}$,即$\frac{1}{1-x}$=$\frac{x}{CN}$,
解得:CN=$\frac{x(1-x)}{1}$=x(1-x),
∴S△ADN=S正方形ABCD=$\frac{1}{2}$×1×[1-x(1-x)]=$\frac{1}{2}$x2-$\frac{1}{2}$x+$\frac{1}{2}$,
∵$\frac{1}{2}$<0,
∴當x=$\frac{1}{2}$cm時,S△ADN最小,最小值是$\frac{4×\frac{1}{2}×\frac{1}{2}-(-\frac{1}{2})^{2}}{4×\frac{1}{2}}$=$\frac{3}{8}$(cm2).
故答案是:$\frac{3}{8}$cm2.
點評 本題考查了二次函數的性質的運用.關鍵是根據已知條件判斷相似三角形,利用相似比求函數關系式.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:選擇題
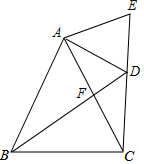 如圖,△ABC中,AB=AC,點F為AC的中點,D為BF的延長線上一點,且∠BDC=∠BAC,E為CD的延長線上一點,且AD=AE,下列結論:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四邊形AEDF.其中結論正確的個數是( )
如圖,△ABC中,AB=AC,點F為AC的中點,D為BF的延長線上一點,且∠BDC=∠BAC,E為CD的延長線上一點,且AD=AE,下列結論:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四邊形AEDF.其中結論正確的個數是( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
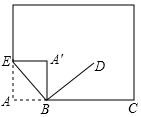 如圖所示,小明將書面折過來,該角頂點A落在A′處,他以折痕BE為一邊作∠DBE=90°,此時小明說BD是∠CBA′的平分線.你認為小明的說法對嗎?說明你的理由.
如圖所示,小明將書面折過來,該角頂點A落在A′處,他以折痕BE為一邊作∠DBE=90°,此時小明說BD是∠CBA′的平分線.你認為小明的說法對嗎?說明你的理由.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 乘法分配律 | B. | 乘法結合律 | ||
| C. | 乘法交換律 | D. | 乘法結合律和交換律 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
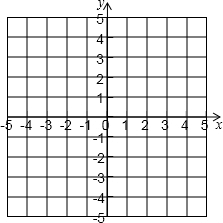 在平面直角坐標系中,將坐標是(0,4),(1,0),(3,0),(4,4)的點用線段依次連接起來形成一個圖案.
在平面直角坐標系中,將坐標是(0,4),(1,0),(3,0),(4,4)的點用線段依次連接起來形成一個圖案. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com