Question

10．如圖，在Rt△ABC中，∠ABC=90°，AB=4，BC=3，點D為AC邊上的動點，點D從點C出發，沿邊CA向A運動，當運動到點A時停止，若設點D運動的速度為每秒1個單位長度，當運動時間t為多少秒時，以點C、B、D為頂點的三角形是等腰三角形？

Answer 1

分析 由勾股定理求出AC，分三種情況：①CD=BD時，∠C=∠DBC，證出BD=AD，得出CD=AD=$\frac{1}{2}$AC=2.5，即可得出結果；②當CD=BC時，CD=3，即可得出結果；③當BD=BC時，過點B作BF⊥AC于F，則CF=DF，由三角形的面積求出BF，由勾股定理求出CF，得出CD，即可得出結果．

解答 解：∵∠ABC=90°，AB=4，BC=3，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5，
分三種情況：
①CD=BD時，∠C=∠DBC，
∵∠C+∠A=∠DBC+∠DBA=90°，
∴∠A=∠DBA，
∴BD=AD，
∴CD=AD=$\frac{1}{2}$AC=2.5，即t=2.5；
②當CD=BC時，CD=3，即t=3；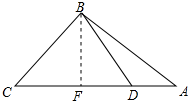
③當BD=BC時，過點B作BF⊥AC于F，如圖所示：
則CF=DF，△ABC的面積=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BF，
∴BF=$\frac{3×4}{5}$=2.4，
∴CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=$\sqrt{{3}^{2}-2．{4}^{2}}$=1.8，
∴CD=3.6，即t=3.6．
綜上所述：當運動時間t為2.5或3或3.6秒時，以點C、B、D為頂點的三角形是等腰三角形．

點評 本題考查了勾股定理、等腰三角形的判定、三角形面積的計算等知識；熟練掌握勾股定理，通過進行分類討論得出結果是解決問題的關鍵．