
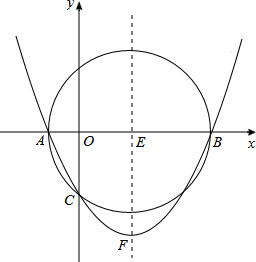 如圖,以E(3,0)為圓心,5為半徑的⊙E與x軸交于A、B兩點,與y軸交于C點,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點,頂點為F.
如圖,以E(3,0)為圓心,5為半徑的⊙E與x軸交于A、B兩點,與y軸交于C點,拋物線y=ax2+bx+c(a≠0)經過A、B、C三點,頂點為F.分析 (1)由題意可直接得到點A、B的坐標,連接CE,在Rt△OCE中,利用勾股定理求出OC的長,則得到點C的坐標;
(2)已知點A、B、C的坐標,利用交點式與待定系數法求出拋物線的解析式,由解析式得到頂點F的坐標;
(3)首先求出點P的坐標;連接EP,PF,過點P作PG⊥對稱軸EF于點G,求出PE,推出點P在⊙E上;再利用勾股定理求出PF的長度,則利用勾股定理的逆定理可判定△EPF為直角三角形,∠EPF=90°,所以直線PF與⊙E相切.
解答 解:(1)∵以E(3,0)為圓心,以5為半徑的⊙E與x軸交于A,B兩點,
∴A(-2,0),B(8,0).
如解答圖所示,連接CE.
在Rt△OCE中,OE=AE-OA=5-2=3,CE=5,
由勾股定理得:OC=$\sqrt{C{E}^{2}-O{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴C(0,-4).
(2)∵點A(-2,0),B(8,0)在拋物線上,
∴可設拋物線的解析式為:y=a(x+2)(x-8).
∵點C(0,-4)在拋物線上,
∴-4=a×2×-8,解得a=$\frac{1}{4}$
∴拋物線的解析式為:y=$\frac{1}{4}$(x+2)(x-8)=$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{1}{4}$(x-3)2-$\frac{25}{4}$,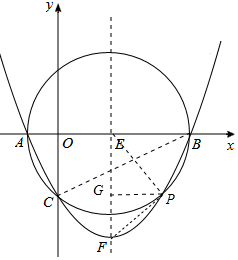
∴頂點F的坐標為(3,-$\frac{25}{4}$).
(3)直線PF與⊙E相切.理由如下:
∵△ABC中,底邊AB上的高OC=4,
∴若△ABC與△ABP面積相等,則拋物線上的點P須滿足條件:|yP|=4,
∵點P在第四象限,
∴yp=-4,則 $\frac{1}{4}$x2-$\frac{3}{2}$x-4=-4,
整理得:x2-6x=0,解得x=6或x=0(與點C重合,故舍去).
∴點P的坐標為(6,-4),連接EP,PF,過點P作PG⊥對稱軸EF于點G,
則PG=3,EG=4.
在Rt△PEG中,由勾股定理得:PE=$\sqrt{E{G}^{2}+P{G}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴點P在⊙E上.
由(2)知,頂點F的坐標(3,-$\frac{25}{4}$),
∴EF=$\frac{25}{4}$,
∴FG=EF-EG=$\frac{9}{4}$.
在Rt△PGF中,由勾股定理得:PF=$\sqrt{P{G}^{2}+G{F}^{2}}$=$\sqrt{{3}^{2}+(\frac{9}{4})^{2}}$=$\frac{15}{4}$.
在△EFP中,∵EP2+PF2=52+( $\frac{15}{4}$)2=( $\frac{25}{4}$)2=EF2,
∴△EFP為直角三角形,∠EPF=90°.
∵點P在⊙E上,且∠EPF=90°,
∴直線PF與⊙E相切.
點評 本題考查圓綜合題、二次函數的圖象與性質、勾股定理及其逆定理、切線的判定、解一元二次方程等知識,解題的關鍵是靈活運用所學知識解決問題,學會添加常用輔助線,構造直角三角形,掌握利用勾股定理的逆定理證明直角的方法,屬于中考壓軸題.


科目:初中數學 來源: 題型:解答題
 如圖,兩幢大樓AB,CD之間的水平距離(BD)為20米,為測得兩幢大樓的高度,小王同學站在大樓AB的頂端A處測得大樓CD頂端C的仰角為60°,測得大樓CD的底部D的俯角為45°,試求大樓AB和CD的高度.(精確到1米)
如圖,兩幢大樓AB,CD之間的水平距離(BD)為20米,為測得兩幢大樓的高度,小王同學站在大樓AB的頂端A處測得大樓CD頂端C的仰角為60°,測得大樓CD的底部D的俯角為45°,試求大樓AB和CD的高度.(精確到1米)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
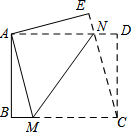 如圖,在長方形ABCD中,AD>AB,將長方形ABCD折疊,使點C與點A重合,折痕為MN,連接CN,若△CDN的面積與△CMN的面積比為1:4,則$\frac{MN}{BM}$的值為( )
如圖,在長方形ABCD中,AD>AB,將長方形ABCD折疊,使點C與點A重合,折痕為MN,連接CN,若△CDN的面積與△CMN的面積比為1:4,則$\frac{MN}{BM}$的值為( )| A. | 5 | B. | 4 | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com