
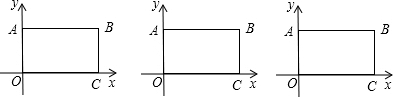
分析 (1)由$\frac{3a+5}{4}$-$\frac{a+3}{2}$=1得到a=5,可得點B坐標(biāo)為(8,5).
(2)當(dāng)0≤t<5時,d=5-t.當(dāng)5≤t≤13時,d=t-5.
(3)分兩種情形討論①如圖1中,當(dāng)點Q是AB中點時,OQ分四邊形OABC的面積為1:3.如圖2中,當(dāng)點Q是BC中點時,OQ分四邊形OABC的面積為1:3,分別求解即可.
解答 解:(1)由$\frac{3a+5}{4}$-$\frac{a+3}{2}$=1得到a=5,
∴點B坐標(biāo)為(8,5).
故答案為(8,5).
(2)當(dāng)0≤t<5時,d=5-t.
當(dāng)5≤t≤13時,d=t-5.
(3)①如圖1中,當(dāng)點Q是AB中點時,OQ分四邊形OABC的面積為1:3,
此時t=$\frac{4}{2}$=2,OP=2,
∴S△POQ=$\frac{1}{2}$×2×4=4.
②如圖2中,當(dāng)點Q是BC中點時,OQ分四邊形OABC的面積為1:3,
此時t=$\frac{12.5}{2}$=$\frac{25}{4}$s,AP=$\frac{25}{4}$-5=$\frac{5}{4}$,PB=8-$\frac{5}{4}$=$\frac{27}{4}$,
∴S△POQ=S矩形OABC-S△AOP-S△PQB-S△OCQ=5×8-$\frac{1}{2}$×5×$\frac{5}{4}$-$\frac{1}{2}$×8×$\frac{5}{2}$-$\frac{1}{2}$×$\frac{5}{2}$×$\frac{27}{4}$=$\frac{295}{16}$.
點評 本題考查三角形綜合題、矩形的性質(zhì)、三角形的面積、一元一次方程等知識,解題的關(guān)鍵是靈活運用所學(xué)知識解決問題,學(xué)會用分類討論的思想思考問題,屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在Rt△ABC中,∠C=90°,AB=10,點D是直角邊AC上一點,且滿足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求線段BD的長度.
如圖,在Rt△ABC中,∠C=90°,AB=10,點D是直角邊AC上一點,且滿足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求線段BD的長度.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $2\sqrt{-8}=-2$ | B. | ${({-\sqrt{2}})^2}=4$ | C. | $\sqrt{{{({-3})}^2}}=-3$ | D. | $\sqrt{16}$=4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
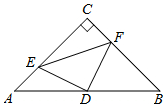 如圖,在△ABC中,∠C=90°,AC=BC=4,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF.在此運動變化的過程中,有下列結(jié)論:①△DFE是等腰直角三角形;②四邊形CEDF不可能為正方形;③四邊形CEDF的面積隨點E位置的改變而發(fā)生變化;④點C、E、D、F四點在同一個圓上,且該圓的面積最小為4π.其中錯誤結(jié)論的個數(shù)是( )個.
如圖,在△ABC中,∠C=90°,AC=BC=4,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF.在此運動變化的過程中,有下列結(jié)論:①△DFE是等腰直角三角形;②四邊形CEDF不可能為正方形;③四邊形CEDF的面積隨點E位置的改變而發(fā)生變化;④點C、E、D、F四點在同一個圓上,且該圓的面積最小為4π.其中錯誤結(jié)論的個數(shù)是( )個.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com