
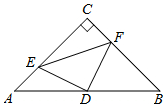
 如圖,在△ABC中,∠C=90°,AC=BC=4,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF.在此運動變化的過程中,有下列結論:①△DFE是等腰直角三角形;②四邊形CEDF不可能為正方形;③四邊形CEDF的面積隨點E位置的改變而發生變化;④點C、E、D、F四點在同一個圓上,且該圓的面積最小為4π.其中錯誤結論的個數是( )個.
如圖,在△ABC中,∠C=90°,AC=BC=4,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF.在此運動變化的過程中,有下列結論:①△DFE是等腰直角三角形;②四邊形CEDF不可能為正方形;③四邊形CEDF的面積隨點E位置的改變而發生變化;④點C、E、D、F四點在同一個圓上,且該圓的面積最小為4π.其中錯誤結論的個數是( )個.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①正確.連接CD.只要證明△ADE≌△CDF(SAS),即可解決問題.
②錯誤.當E、F分別為AC、BC中點時,四邊形CEDF為正方形.
③錯誤.四邊形CEDF的面積=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4,為定值.
④錯誤.以EF為直徑的圓的面積的最小值=π•( $\frac{1}{2}$•2 $\sqrt{2}$)2=2π.
解答 解:連接CD,如圖1,
∵∠C=90°,AC=BC=4,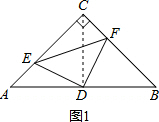
∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∵D為AB的中點,
∴CD⊥AB,CD=AD=BD,
∴∠DCB=∠B=45°,
∴∠A=∠DCF,
在△ADE和△CDF中
$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,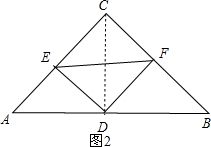
∴△ADE≌△CDF(SAS),
∴ED=DF,∠CDF=∠ADE,
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=90°,即∠EDF=90°,
∴△DFE是等腰直角三角形,所以①正確;
當E、F分別為AC、BC中點時,如圖2,則AE=CE=CF=BF,DE=AE=CE,
∴CE=CF=DE=DF,
而∠ECF=90°,
∴四邊形CDFE是正方形,所以②錯誤;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四邊形CEDF=S△CDE+S△CDF=S△CDE+S△ADE=S△ADC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4,所以③錯誤;
∵△CEF和△DEF都為直角三角形,
∴點C、D在以EF為直徑的圓上,即點C、E、D、F四點在同一個圓上,
∵△DEF是等腰直角三角形,
∴EF=$\sqrt{2}$DE,
當DE⊥AC時,DE最短,此時DE=$\frac{1}{2}$AC=2,
∴EF的最小值為2 $\sqrt{2}$,
∴以EF為直徑的圓的面積的最小值=π•( $\frac{1}{2}$•2 $\sqrt{2}$)2=2π,所以④錯誤;
故選C.
點評 本題考查三角形的綜合題、等腰直角三角形的判定與性質、直角三角形斜邊上的中線性質、全等三角形的判定和性質等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考壓軸題.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:解答題
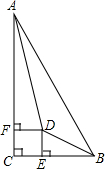 已知:如圖,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分線相交于點D,DE⊥BC,DF⊥AC,垂足分別為E、F.求證:四邊形CEDF是正方形.
已知:如圖,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分線相交于點D,DE⊥BC,DF⊥AC,垂足分別為E、F.求證:四邊形CEDF是正方形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
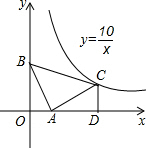 如圖,在等腰直角三角形ABC中,∠BAC=90°,點A在x軸上,點B的坐標是(0,3).若點C恰好在反比例函數y=$\frac{10}{x}$第一象限內的圖象上,過點C作CD⊥x軸于點D,那么點C的坐標為(5,2).
如圖,在等腰直角三角形ABC中,∠BAC=90°,點A在x軸上,點B的坐標是(0,3).若點C恰好在反比例函數y=$\frac{10}{x}$第一象限內的圖象上,過點C作CD⊥x軸于點D,那么點C的坐標為(5,2).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 點P的⊙O外 | B. | 點P的⊙O上 | C. | 點P的⊙O內 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 價目表 | |
| 不超過200度的部分 | 0.50元/度 |
| 超過200度不超過400度的部分 | a元/度 |
| 超過400度的部分 | 0.80元/度 |
| 注:電費按月結算 | |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com