
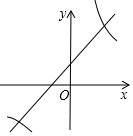
 反比例函數y=$\frac{6}{x}$與一次函數y=x+1的圖象交于點A(2,3),利用圖象的對稱性可知它們的另一個交點是(-3,2),$\frac{6}{x}$<x+1的解集為-3<x<0或x>2.
反比例函數y=$\frac{6}{x}$與一次函數y=x+1的圖象交于點A(2,3),利用圖象的對稱性可知它們的另一個交點是(-3,2),$\frac{6}{x}$<x+1的解集為-3<x<0或x>2. 分析 求出直線y=x+1與直線y=-x的交點坐標,由反比例函數與一次函數均關于直線y=-x對稱,結合點A的坐標即可求出另一交點坐標,再根據兩函數圖象的上下位置關系結合兩交點的橫坐標即可得出不等式的解集.
解答 解:令y=x+1=-x,
解得:x=-$\frac{1}{2}$,y=-x=$\frac{1}{2}$.
∵反比例函數y=$\frac{6}{x}$和一次函數y=x+1的圖象均關于直線y=-x對稱,
∴反比例函數y=$\frac{6}{x}$與一次函數y=x+1的圖象交點關于點(-$\frac{1}{2}$,$\frac{1}{2}$)對稱,
∴另一交點的坐標為(-$\frac{1}{2}$×2-2,$\frac{1}{2}$×2-3),即(-3,-2).
觀察函數圖象可知:當-3<x<0或x>2時,反比例函數圖象在一次函數圖象下方,
∴不等式$\frac{6}{x}$<x+1的解集為-3<x<0或x>2.
故答案為:2;-3<x<0或x>2.
點評 本題考查了反比例函數與一次函數的交點問題以及函數圖象,根據兩函數圖象的上下位置關系找出不等式的解集是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知,如圖,⊙O是△ABC的外接圓,OD⊥BC交⊙O于點D,CE平分∠ACB交AB于點E,交⊙O于點H,AD與CH相交于點G,延長CH到點M,使MH=HG,延長DA到點K,使AK=AG,CA的延長線交MK于點F,求證:ME=MF.
已知,如圖,⊙O是△ABC的外接圓,OD⊥BC交⊙O于點D,CE平分∠ACB交AB于點E,交⊙O于點H,AD與CH相交于點G,延長CH到點M,使MH=HG,延長DA到點K,使AK=AG,CA的延長線交MK于點F,求證:ME=MF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,兩個半徑都是4cm的圓外切于點C,一只螞蟻由點A開始依次A、B、C、D、E、F、C、G、A這8段路徑上不斷爬行,直到行走2006πcm后才停下來,則螞蟻停的那一個點為( )
如圖,兩個半徑都是4cm的圓外切于點C,一只螞蟻由點A開始依次A、B、C、D、E、F、C、G、A這8段路徑上不斷爬行,直到行走2006πcm后才停下來,則螞蟻停的那一個點為( )| A. | D點 | B. | E點 | C. | F點 | D. | G點 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
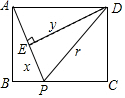 如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )
如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )| A. | 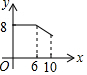 | B. | 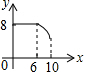 | C. |  | D. | 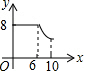 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com