
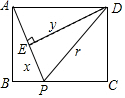
 如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )
如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )| A. | 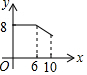 | B. | 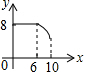 | C. |  | D. | 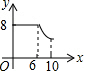 |
分析 ①點P在AB上時,點D到AP的距離為AD的長度,②點P在BC上時,根據同角的余角相等求出∠APB=∠PAD,再利用相似三角形的性質列出比例式整理得到y與x的關系式,從而得解.
解答  解:①點P在AB上時,0≤x≤6,點D到AP的距離為AD的長度,是定值8;
解:①點P在AB上時,0≤x≤6,點D到AP的距離為AD的長度,是定值8;
②點P在BC上時,6<x≤10,
∵∠APB+∠BAP=90°,
∠PAD+∠BAP=90°,
∴∠APB=∠PAD,
又∵∠B=∠DEA=90°,
∴△ABP∽△DEA,
∴$\frac{AB}{DE}$=$\frac{AP}{AD}$,
即$\frac{6}{y}$=$\frac{x}{8}$,
∴y=$\frac{24}{x}$,
縱觀各選項,只有D選項圖形符合.
故選:D.
點評 本題考查了動點問題函數圖象,關鍵是利用了相似三角形的判定與性質,難點在于根據點P的位置分兩種情況討論.


科目:初中數學 來源: 題型:填空題
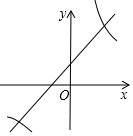 反比例函數y=$\frac{6}{x}$與一次函數y=x+1的圖象交于點A(2,3),利用圖象的對稱性可知它們的另一個交點是(-3,2),$\frac{6}{x}$<x+1的解集為-3<x<0或x>2.
反比例函數y=$\frac{6}{x}$與一次函數y=x+1的圖象交于點A(2,3),利用圖象的對稱性可知它們的另一個交點是(-3,2),$\frac{6}{x}$<x+1的解集為-3<x<0或x>2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
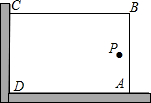 我縣一小區為了美化環境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)
我縣一小區為了美化環境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6 | B. | 5 | C. | $\frac{5}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
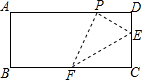 如圖,在矩形ABCD中,點E、F分別在邊CD和BC上,且CD=4DE=4a,將矩形沿直線EF折疊,使點C恰好落在AD邊上點P處,則FP=3$\sqrt{2}$a.
如圖,在矩形ABCD中,點E、F分別在邊CD和BC上,且CD=4DE=4a,將矩形沿直線EF折疊,使點C恰好落在AD邊上點P處,則FP=3$\sqrt{2}$a.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
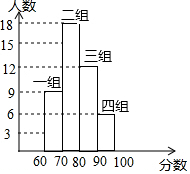 某校七(3)班的同學進行了一次安全知識測試,測試成績進行整理后分成四個組,并繪制如圖所示的頻數直方圖,則第二組的頻數是( )
某校七(3)班的同學進行了一次安全知識測試,測試成績進行整理后分成四個組,并繪制如圖所示的頻數直方圖,則第二組的頻數是( )| A. | 0.4 | B. | 18 | C. | 0.6 | D. | 27 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
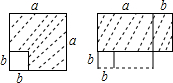 如圖,在邊長為a的正方形中挖掉一個邊長為b的小正方形(a>b),把余下的部分剪拼成為一個矩形,通過計算兩個圖形(陰影部分)的面積,可以驗證的等式是( )
如圖,在邊長為a的正方形中挖掉一個邊長為b的小正方形(a>b),把余下的部分剪拼成為一個矩形,通過計算兩個圖形(陰影部分)的面積,可以驗證的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com