
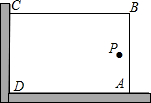
 我縣一小區為了美化環境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)
我縣一小區為了美化環境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)分析 (1)根據題意可以列出面積與x的關系式,然后由花園的面積為180m2,可以求得相應的x的值;
(2)由題意可知AB≥5,CB≥16,從而可以得到x的取值范圍,然后進行討論,即可求得花園面積S的最大值.
解答 解:設AB=xm,則BC=(28-x)m
(1)由題意得x(28-x)=180,
解得:x1=10,x2=18,
答:AB的長為10m或18m;
(2)由題意,$\left\{\begin{array}{l}{x≥6}\\{28-x≥16}\end{array}\right.$,
解得,5≤x≤12,
∵花園面積S=x(28-x)=-(x-14)2+196
∴x≤14時,S隨x的增大而增大.
∴當x=12時,花園的面積取得最大值,
S最大=-(12-14)2+196=192(m2),
即在P處有一棵樹與墻CD,AD的距離分別是16m和5m,要將這棵樹圍在花園內(含邊界,不考慮樹的粗細),花園面積S的最大值是192m2.
點評 本題考查二次函數的應用,一元一次方程的應用,解題的關鍵是明確題意列出相應的關系式,找出所求問題需要的條件.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖1,A、B、C三點在正方形網格線的交點處,若將△ACB逆時針旋轉得到△AC′B′,則tanB′的值為( )
如圖1,A、B、C三點在正方形網格線的交點處,若將△ACB逆時針旋轉得到△AC′B′,則tanB′的值為( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在平面直角坐標系中,Rt△ABC的頂點B在原點O,直角邊BC在x軸的正半軸上,∠ACB=90°,點A的坐標為(3,$\sqrt{3}$),點D是BC邊上一個動點(不與點B,C重合),過點D作DE⊥BC交AB邊于點E,將∠ABC沿直線DE翻折,點B落在x軸上的點F處當△AEF為直角三角形時,點F的坐標是(2,0)或(4,0).
如圖,在平面直角坐標系中,Rt△ABC的頂點B在原點O,直角邊BC在x軸的正半軸上,∠ACB=90°,點A的坐標為(3,$\sqrt{3}$),點D是BC邊上一個動點(不與點B,C重合),過點D作DE⊥BC交AB邊于點E,將∠ABC沿直線DE翻折,點B落在x軸上的點F處當△AEF為直角三角形時,點F的坐標是(2,0)或(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
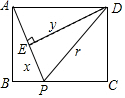 如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )
如圖,矩形ABCD中,AB=6,BC=8,動點P從點A出發,按A→B→C的方向在AB和BC上移動,記PA=x,點D到直線PA的距離為y,則y關于x的函數圖象大致是( )| A. | 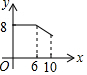 | B. | 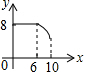 | C. |  | D. | 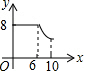 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com