
 如圖,在平面直角坐標(biāo)系中,Rt△ABC的頂點B在原點O,直角邊BC在x軸的正半軸上,∠ACB=90°,點A的坐標(biāo)為(3,$\sqrt{3}$),點D是BC邊上一個動點(不與點B,C重合),過點D作DE⊥BC交AB邊于點E,將∠ABC沿直線DE翻折,點B落在x軸上的點F處當(dāng)△AEF為直角三角形時,點F的坐標(biāo)是(2,0)或(4,0).
如圖,在平面直角坐標(biāo)系中,Rt△ABC的頂點B在原點O,直角邊BC在x軸的正半軸上,∠ACB=90°,點A的坐標(biāo)為(3,$\sqrt{3}$),點D是BC邊上一個動點(不與點B,C重合),過點D作DE⊥BC交AB邊于點E,將∠ABC沿直線DE翻折,點B落在x軸上的點F處當(dāng)△AEF為直角三角形時,點F的坐標(biāo)是(2,0)或(4,0). 分析 分兩種情討論即可①如圖1中,當(dāng)∠AFE=90°,在Rt△ACF中,求出CF即可.如圖2中,當(dāng)∠EAF=90°時,在Rt△ACF中,求出CF即可.
解答 解:①如圖1中,當(dāng)∠AFE=90°,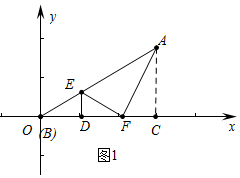
∵A(3,$\sqrt{3}$),
∴OC=3,AC=$\sqrt{3}$,
∴tan∠AOC=$\frac{AC}{OC}$=$\frac{\sqrt{3}}{3}$,
∴∠AOC=30°,
∵EO=EF,
∴∠EOF=∠EFO=30°,
∴∠AEF=∠EOF+∠EFO=60°,
∴∠EAF=∠FAC=30°,
∴CF=AC•tan30°=1,
∴OF=OC-CF=2,
∴F(2,0).
②如圖2中,當(dāng)∠EAF=90°時,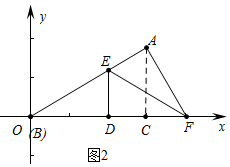
易知∠CAF=30°,
CF=AC•tan30°=1,
∴OF=OC+CF=4,
∴F(4,0),
③∠AEF=60°,不可能為90°.
故答案為(2,0)或(4,0).
點評 本題考查翻折變換、坐標(biāo)與圖形的變化、銳角三角函數(shù)等知識,解題的關(guān)鍵是學(xué)會用分類討論的思想思考問題,屬于中考常考題型.


科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
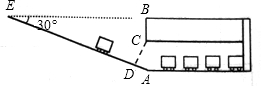 某校九年級數(shù)學(xué)興趣小組為了測得該校地下停車場的限高CD(CD⊥AE),在課外活動時間測得下列數(shù)據(jù):如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米,試求該校地下停車場的高度AC及限高CD($\sqrt{3}$≈1.73,結(jié)果精確到0.1米)
某校九年級數(shù)學(xué)興趣小組為了測得該校地下停車場的限高CD(CD⊥AE),在課外活動時間測得下列數(shù)據(jù):如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米,試求該校地下停車場的高度AC及限高CD($\sqrt{3}$≈1.73,結(jié)果精確到0.1米)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
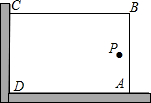 我縣一小區(qū)為了美化環(huán)境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)
我縣一小區(qū)為了美化環(huán)境,打算借助如圖所示的直角墻角(兩邊足夠長),用28m長的圍欄圍成一個矩形花園ABCD(圍欄只圍AB、BC兩邊)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
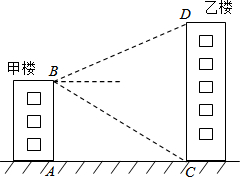 如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂?shù)腂處看乙樓樓頂?shù)腄處,仰角為28°,求乙樓的高CD的長.(結(jié)果精確到0.1m,參考數(shù)據(jù):sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂?shù)腂處看乙樓樓頂?shù)腄處,仰角為28°,求乙樓的高CD的長.(結(jié)果精確到0.1m,參考數(shù)據(jù):sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 6 | B. | 5 | C. | $\frac{5}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
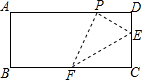 如圖,在矩形ABCD中,點E、F分別在邊CD和BC上,且CD=4DE=4a,將矩形沿直線EF折疊,使點C恰好落在AD邊上點P處,則FP=3$\sqrt{2}$a.
如圖,在矩形ABCD中,點E、F分別在邊CD和BC上,且CD=4DE=4a,將矩形沿直線EF折疊,使點C恰好落在AD邊上點P處,則FP=3$\sqrt{2}$a.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
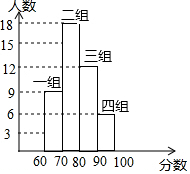 某校七(3)班的同學(xué)進(jìn)行了一次安全知識測試,測試成績進(jìn)行整理后分成四個組,并繪制如圖所示的頻數(shù)直方圖,則第二組的頻數(shù)是( )
某校七(3)班的同學(xué)進(jìn)行了一次安全知識測試,測試成績進(jìn)行整理后分成四個組,并繪制如圖所示的頻數(shù)直方圖,則第二組的頻數(shù)是( )| A. | 0.4 | B. | 18 | C. | 0.6 | D. | 27 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
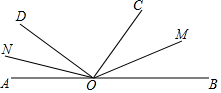 如圖,點O在直線AB上,射線OC、OD在直線AB的同側(cè),∠AOD=40°,∠BOC=50°,OM、ON分別平分∠BOC和∠AOD,則∠MON的度數(shù)為( )
如圖,點O在直線AB上,射線OC、OD在直線AB的同側(cè),∠AOD=40°,∠BOC=50°,OM、ON分別平分∠BOC和∠AOD,則∠MON的度數(shù)為( )| A. | 135° | B. | 140° | C. | 152° | D. | 45° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com