
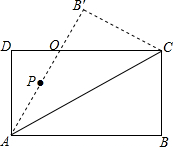
 如圖,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,將△ABC沿AC邊翻折,使點(diǎn)B到點(diǎn)B′,AB′與DC相交于點(diǎn)O.
如圖,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,將△ABC沿AC邊翻折,使點(diǎn)B到點(diǎn)B′,AB′與DC相交于點(diǎn)O.分析 (1)先判斷出∠DAO=∠BAC即可得出結(jié)論;
(2)先表示出AP,用三角形的面積公式直接得出結(jié)論;
(3)先表示出AP,B'P,分三種情況用勾股定理建立方程求解即可.
解答 解:(1)在矩形ABCD中,∠ABC=∠ADC=∠BAD=90°,
∵∠CAB=30°,
∴∠CAD=60°,
由折疊得,∠B'AC=∠CAB=30°,
∴∠DAO=∠CAD-∠B'AC=30°=∠BAC,
∵∠ADO=∠ABC=90°,
∴△ADO∽△ABC;
(2)如圖,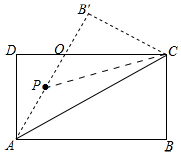 連接PC,
連接PC,
在Rt△ABC中,∠BAC=30°,BC=4$\sqrt{3}$,
∴AB=$\sqrt{3}$BC=12,
由折疊知AB'=AB=12,
由運(yùn)動(dòng)知,AP=2t,
由折疊得,B'C=BC=4$\sqrt{3}$cm,
∴S=S△APC=$\frac{1}{2}$AP•B'C=$\frac{1}{2}$×2t×4$\sqrt{3}$=4$\sqrt{3}$t(0<t≤6);
(3)能構(gòu)成直角三角形,
由運(yùn)動(dòng)知,AP=2t,B'P=AB'-AP=12-2t,
∵以AP、B′P、BC的長(zhǎng)為邊構(gòu)成直角三角形,
∴①AP2+B'P2=BC2,
∴(2t)2+(12-2t)2=48,
∴此方程無解;
②AP2+BC2=B'P2,
∴(2t)2+48=(12-2t)2,
∴t=2,
∴AP=2t=4cm,此時(shí),點(diǎn)P在AB'上距點(diǎn)A4cm處
③B'P2+BC2=AP2,(12-2t)2+48=(2t)2,
∴t=4,
∴AP=2t=8cm,此時(shí),點(diǎn)P在AB'上,距點(diǎn)A8cm處.
即:點(diǎn)p距點(diǎn)A是4cm和8cm處時(shí),以AP、B′P、BC的長(zhǎng)為邊構(gòu)成直角三角形.
點(diǎn)評(píng) 此題主要考查了相似三角形的性質(zhì)和判定,折疊的性質(zhì),勾股定理,三角形的面積公式,解(1)的關(guān)鍵是判斷出∠DAO=∠BAC,解(3)的關(guān)鍵是關(guān)鍵勾股定理建立方程.


 全能測(cè)控期末小狀元系列答案
全能測(cè)控期末小狀元系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在△ABC和△DEF中,點(diǎn)B,F(xiàn),C,E在同一直線上,BF=CE,AC=DF,AC∥DF. 求證:
如圖,在△ABC和△DEF中,點(diǎn)B,F(xiàn),C,E在同一直線上,BF=CE,AC=DF,AC∥DF. 求證:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,連接EF.求證:
如圖,在Rt△ABC中,∠BAC=90°,AG⊥BC于G,BD平分∠ABC,AE⊥BD于H,交BC于E,AG交BD于F,連接EF.求證:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一點(diǎn)O為圓心OA為半徑作⊙O,若⊙O與邊BC始終有交點(diǎn)(包括B、C兩點(diǎn)),則線段AO的取值范圍是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.
如圖,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一點(diǎn)O為圓心OA為半徑作⊙O,若⊙O與邊BC始終有交點(diǎn)(包括B、C兩點(diǎn)),則線段AO的取值范圍是$\sqrt{3}≤OA≤\frac{4}{3}\sqrt{3}$.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com