
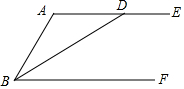
 已知BD平分∠ABF,且交AE于點D.
已知BD平分∠ABF,且交AE于點D.分析 (1)根據(jù)角平分線的作法作出∠BAE的平分線AP即可;
(2)根據(jù)ASA證明△ABO≌△CBO,得出AO=CO,AB=CB,再根據(jù)ASA證明△ABO≌△ADO,得出BO=DO.由對角線互相平分的四邊形是平行四邊形及有一組鄰邊相等的平行四邊形是菱形即可證明四邊形ABCD是菱形即可得.
解答 解:(1)如圖所示: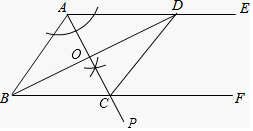
(2)在△ABO和△CBO中,
∵$\left\{\begin{array}{l}{∠ABO=∠CBO}\\{OB=OB}\\{∠AOB=∠COB=90°}\end{array}\right.$,
∴△ABO≌△CBO(ASA),
∴AO=CO,AB=CB.
在△ABO和△ADO中,
∵$\left\{\begin{array}{l}{∠OAB=∠OAD}\\{OA=OA}\\{∠AOB=∠AOD=90°}\end{array}\right.$,
∴△ABO≌△ADO(ASA),
∴BO=DO.
∵AO=CO,BO=DO,
∴四邊形ABCD是平行四邊形,
∵AB=CB,
∴平行四邊形ABCD是菱形,
∴AD與BC的位置和數(shù)量關(guān)系是:平行且相等,
故答案為:平行且相等.
點評 此題主要考查了角平分線的作法以及菱形的判定和全等三角形的判定與性質(zhì),熟練掌握菱形的判定是解題關(guān)鍵.


 同步練習(xí)強化拓展系列答案
同步練習(xí)強化拓展系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
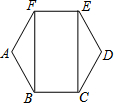 如圖,在正六邊形ABCDEF中,四邊形BCEF的面積為30,則正六邊形ABCDEF的面積為( )
如圖,在正六邊形ABCDEF中,四邊形BCEF的面積為30,則正六邊形ABCDEF的面積為( )| A. | 20$\sqrt{3}$ | B. | 40 | C. | 20$\sqrt{5}$ | D. | 45 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
 在△ABC中,點D,E分別在AB,AC上,且CD與BE相交于點F,已知△BDF的面積為6,△BCF的面積為9,△CEF的面積為6,則四邊形ADFE的面積為24.
在△ABC中,點D,E分別在AB,AC上,且CD與BE相交于點F,已知△BDF的面積為6,△BCF的面積為9,△CEF的面積為6,則四邊形ADFE的面積為24.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
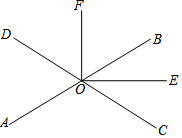 如圖所示,直線AB,CD相交于點O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度數(shù).
如圖所示,直線AB,CD相交于點O,OE平分∠BOC,OF⊥OE,且∠AOC=114°,求∠BOF的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com