
分析 (1)先確定拋物線y=-3x2-12x-14的頂點坐標(biāo),然后根據(jù)中心對稱的性質(zhì)求得原拋物線的頂點坐標(biāo),即可求得解析式;由頂點坐標(biāo)得出頂點沿x軸的正方向平移2個單位,沿y軸的正方向平移2個單位,從而求得沿直線y=x方向平移的距離.
(2)求得當(dāng)1≤x≤5時,函數(shù)y=3x2-12x+14的最大值,即可求得代數(shù)式$\frac{1}{a{x}^{2}+bx+c}$的最小值.
解答 解:(1)∵y=-3x2-12x-14=-3(x+2)2-2,
∴頂點為(-2,-2),
∵拋物線y=-3x2-12x-14與原拋物線關(guān)于原點中心對稱,
∴原拋物線的頂點為(2,2),
∴原拋物線的解析式為y=3(x-2)2+2,
即y=3x2-12x+14.
由頂點坐標(biāo)可知,頂點沿x軸的正方向平移2個單位,沿y軸的正方向平移2個單位,
∴沿直線y=x方向平移了4$\sqrt{2}$個單位.
(2)把x=1代入y=3x2-12x+14得,y=5,
把x=5代入y=3x2-12x+14得,y=29,
∴1≤x≤5時,函數(shù)y=3x2-12x+14的最大值為29,
∴代數(shù)式$\frac{1}{a{x}^{2}+bx+c}$的最小值為$\frac{1}{29}$.
點評 本題考查了二次函數(shù)圖象與幾何變換,一次函數(shù)圖象上點的坐標(biāo)特征,二次函數(shù)的最值以及中心對稱的性質(zhì),得出頂點坐標(biāo)是解題的關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:解答題
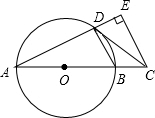 如圖,AB是⊙O的直徑,點C在AB的延長線上,CD與⊙O相切于點D,CE⊥AD,交AD的延長線于點E.
如圖,AB是⊙O的直徑,點C在AB的延長線上,CD與⊙O相切于點D,CE⊥AD,交AD的延長線于點E.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
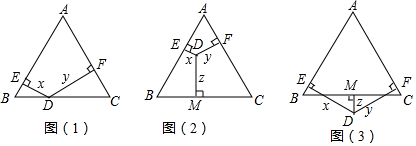
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
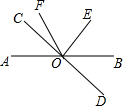 如圖,已知直線AB和CD相交于點O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度數(shù).
如圖,已知直線AB和CD相交于點O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
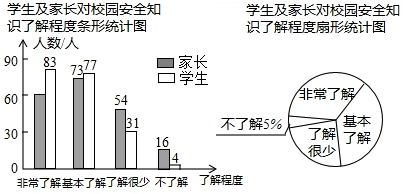
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com