
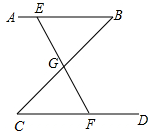
 如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理.
如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理. 分析 根據兩直線平行,內錯角相等可得∠B=∠C,然后利用“角邊角”證明△CFG和△BEG全等,根據全等三角形對應邊相等可得EG=FG,從而得解.
解答 解:測量出E、G之間的距離即為G、F之間的距離.
理由如下:∵AB∥CD,
∴∠B=∠C,
∵G恰好為BC的中點,
∴BG=CG,
在△CFG和△BEG中,$\left\{\begin{array}{l}{∠B=∠C}\\{BG=CG}\\{∠BGE=∠CGF}\end{array}\right.$,
∴△CFG≌△BEG(ASA),
∴EG=FG,
故,E、G之間的距離即為G、F之間的距離.
點評 本題考查了全等三角形的應用,平行線的性質,熟練掌握三角形全等的判定方法并準確識圖確定出全等三角形是解題的關鍵.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:選擇題
| A. | 三角形的內心到三角形三條邊的距離相等 | |
| B. | 三角形三條邊的垂直平分線的交點到三角形三個頂點的距離相等 | |
| C. | 對于實數a,b,若|a|≤|b|,則a≤b | |
| D. | 對于實數x,若$\sqrt{{x}^{2}}$=x,則x≥0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ∠D=90° | B. | AC=BD | C. | AB=AC | D. | 以上都不行 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| x | 3 | 5 | 7 |
| y | 0.08 | 0.08 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 一次性購物 | 優惠方法 |
| 少于200元 | 不予優惠 |
| 低于500元但不低于200元 | 九折優惠 |
| 500元或超過500元 | 其中500元部分給予九折優惠,超過500元部分給予八折優惠 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com