
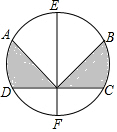
 如圖A,B,C,D,E,F把半徑為3厘米的圓6等分,則陰影部分的面積為( )
如圖A,B,C,D,E,F把半徑為3厘米的圓6等分,則陰影部分的面積為( )| A. | 9π | B. | 3π | C. | 6π | D. | $\frac{9}{4}$π |
分析 先設EF的中點為O,則O為圓心,連接OA,OB,OC,OD,再判定△BOC是等邊三角形,得出∠BOE=∠OBC,BC=BO=CO=3,進而得到BC∥EF,可得△BCG面積=△BCO面積,故扇形BOC的面積=EF右邊陰影部分的面積,根據EF右邊陰影部分的面積=$\frac{3}{2}π$,可得圖中陰影部分的面積.
解答 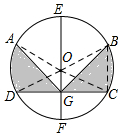 解:設EF的中點為O,則O為圓心,
解:設EF的中點為O,則O為圓心,
連接OA,OB,OC,OD,
∵A,B,C,D,E,F把半徑為3厘米的圓6等分,
∴∠EOB=∠BOC=∠CPF=60°,
又∵OB=OC,
∴△BOC是等邊三角形,
∴∠BOE=∠OBC,BC=BO=CO=3,
∴BC∥EF,
∴△BCG面積=△BCO面積,
∴扇形BOC的面積=EF右邊陰影部分的面積,
又∵扇形BOC的面積=$\frac{60×π×{3}^{2}}{360}$=$\frac{3}{2}π$,
∴EF右邊陰影部分的面積=$\frac{3}{2}π$,
同理可得,EF左邊陰影部分的面積=$\frac{3}{2}π$,
∴陰影部分的面積為3π.
故選:B.
點評 本題主要考查了扇形面積以及等邊三角形的性質的運用,解決問題的關鍵是掌握:由組成圓心角的兩條半徑和圓心角所對的弧所圍成的圖形叫做扇形.求陰影面積的主要思路是將不規則圖形面積轉化為規則圖形的面積.


科目:初中數學 來源: 題型:選擇題
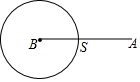 如圖,動點S從點A出發,沿線段AB運動至點B后,立即按原路返回,點S在運動過程中速度不變,則以點B為圓心,線段BS長為半徑的圓的面積m與點S的運動時間t之間的函數關系圖象大致為( )
如圖,動點S從點A出發,沿線段AB運動至點B后,立即按原路返回,點S在運動過程中速度不變,則以點B為圓心,線段BS長為半徑的圓的面積m與點S的運動時間t之間的函數關系圖象大致為( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=15 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=15 | C. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{4}$ | D. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 最高分 | B. | 中位數 | C. | 極差 | D. | 平均數 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
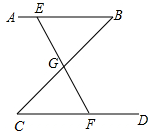 如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理.
如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 到C地 | 到D地 | |
| A果園 | 每噸15元 | 每噸12元 |
| B果園 | 每噸10元 | 每噸9元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
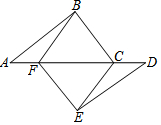 如圖,點A、F、C、D在同一條直線上,點B和點E分別在直線AD的兩側,且AB=DE,∠BAD=∠ADE,AF=DC.求證:四邊形BCEF是平行四邊形.
如圖,點A、F、C、D在同一條直線上,點B和點E分別在直線AD的兩側,且AB=DE,∠BAD=∠ADE,AF=DC.求證:四邊形BCEF是平行四邊形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com