
| x | 3 | 5 | 7 |
| y | 0.08 | 0.08 | 3 |
分析 把x=3,y=0.08;x=5,y=0.08可確定拋物線的對稱軸為直線x=4,利用拋物線的對稱性得到x=1時,y=3,即a+b+c=3,然后利用整體代入的方法計算(a+b+c)($\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)的值.
解答 解:∵x=3,y=0.08;x=5,y=0.08,
∴拋物線的對稱軸為x=-$\frac{b}{2a}$=$\frac{3+5}{2}$=4,
∴-$\frac{b}{a}$=8,
∴x=1與x=7時的函數值相等,
∴x=1時,y=3,即a+b+c=3,
∴(a+b+c)($\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$+$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$)=3×(-$\frac{b}{a}$)=3×8=24.
故答案為:24.
點評 本題考查了二次函數圖形上點的坐標特征:利用拋物線上的點滿足拋物線解析式,可判斷點是否在拋物線上或確定點的坐標.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案科目:初中數學 來源: 題型:選擇題
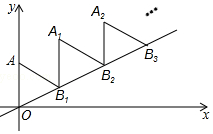 如圖,放置的△OAB1,△B1A1B2,△B2A2B3,…都是邊長為2的等邊三角形,邊AO在Y軸上,點B1、B2、B3…都在直線y=$\frac{\sqrt{3}}{3}$x上,則點A2016的坐標為( )
如圖,放置的△OAB1,△B1A1B2,△B2A2B3,…都是邊長為2的等邊三角形,邊AO在Y軸上,點B1、B2、B3…都在直線y=$\frac{\sqrt{3}}{3}$x上,則點A2016的坐標為( )| A. | (2016$\sqrt{3}$,2018) | B. | (2016$\sqrt{3}$,2016) | C. | (2016,2016$\sqrt{3}$) | D. | (2016,2018$\sqrt{3}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=15 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=15 | C. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{4}$ | D. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
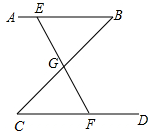 如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理.
如圖,公園里有一條“Z”形的林蔭小道ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一條石凳E、G、F,且G恰好為BC的中點,E、G、F三點在同一條直線上,點G與F之間有一座假山,而使得兩處不能直接到達.你能想出測量G、F之間距離的方法嗎?說明其中的道理.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 到C地 | 到D地 | |
| A果園 | 每噸15元 | 每噸12元 |
| B果園 | 每噸10元 | 每噸9元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
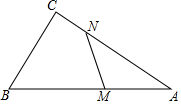 已知,在△ACB中,BC=9,AC=12,AB=15.若線段AB上有一點動點M,線段AC上有一動點N,始終保持AM=CN,若△AMN是直角三角形,且MN=4,則AM的長為$\frac{16}{3}$.
已知,在△ACB中,BC=9,AC=12,AB=15.若線段AB上有一點動點M,線段AC上有一動點N,始終保持AM=CN,若△AMN是直角三角形,且MN=4,則AM的長為$\frac{16}{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com