
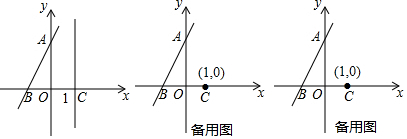
分析 (1)設(shè)直線l的解析式為y=$\sqrt{3}$x+b,把點(diǎn)C(1,0)坐標(biāo)代入求出b即可.
(2)①求出點(diǎn)A的坐標(biāo),利用兩點(diǎn)間距離公式即可求出AC的長(zhǎng).②如圖1中,由CE∥OA,推出∠ACE=∠ACO,由tan∠OAC=$\frac{OC}{OA}$=$\frac{\sqrt{3}}{3}$,推出∠ACO=30°,由此即可解決問(wèn)題.
(3)由圖2、圖3、圖4、圖5可知,當(dāng)α=15°或60°或105°或150°時(shí),△ABD、△ACD、△BCD均為等腰三角形.
解答 解:(1)當(dāng)直線l與直線y=$\sqrt{3}$x+$\sqrt{3}$平行時(shí),設(shè)直線l的解析式為y=$\sqrt{3}$x+b,
∵直線l經(jīng)過(guò)點(diǎn)C(1,0),
∴0=$\sqrt{3}$+b,
∴b=-$\sqrt{3}$,
∴直線l的解析式為y=$\sqrt{3}$x-$\sqrt{3}$.
(2)對(duì)于直線y=$\sqrt{3}$x+$\sqrt{3}$令x=0得y=$\sqrt{3}$,令y=0得x=-1,
∴A(0,$\sqrt{3}$),B(-1,0),∵C(1,0),
∴AC=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
如圖1中,
∵CE∥OA,
∴∠ACE=∠ACO,
∵tan∠OAC=$\frac{OC}{OA}$=$\frac{\sqrt{3}}{3}$,
∴∠ACO=30°,
∴∠ACE=30°,
∴α=30°.
(3)由圖2、圖3、圖4、圖5可知,當(dāng)α=15°或60°或105°或150°時(shí),△ABD、△ACD、△BCD均為等腰三角形.



①如圖2中,當(dāng)α=15°時(shí),
∵CE∥OD,
∴∠ODC=15°,
∵∠OAC=30°,
∴∠ACD=∠ADC=15°,
∴AD=AC=AB,
∴△ADB,△ADC是等腰三角形,
∵OD垂直平分BC,
∴DB=DC,
∴△DBC是等腰三角形.
②當(dāng)α=60°時(shí),易知∠DAC=∠DCA=30°,
∴DA=DC=DB,
∴△ABD、△ACD、△BCD均為等腰三角形.
③當(dāng)α=105°時(shí),易知∠ABD=∠ADB=∠ADC=∠ACD=75°,∠DBC=∠DCB=15°,
∴△ABD、△ACD、△BCD均為等腰三角形.
④當(dāng)α=150°時(shí),易知△BDC是等邊三角形,
∴AB=BD=DC=AC,
∴△ABD、△ACD、△BCD均為等腰三角形.
點(diǎn)評(píng) 本題考查一次函數(shù)綜合題、兩直線平行的條件、銳角三角函數(shù)、勾股定理、等腰三角形的判定和性質(zhì)等知識(shí),解題的關(guān)鍵是靈活運(yùn)用所學(xué)知識(shí)解決問(wèn)題,屬于中考常考題型.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
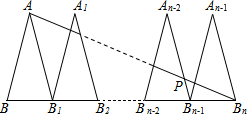 如圖,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n個(gè)全等的等腰三角形,其中AB=2,BB1=1,底邊BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一條直線上,連接ABn交An-2Bn-1于點(diǎn)P,則PBn-1的值為$\frac{2}{n-1}$.
如圖,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n個(gè)全等的等腰三角形,其中AB=2,BB1=1,底邊BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一條直線上,連接ABn交An-2Bn-1于點(diǎn)P,則PBn-1的值為$\frac{2}{n-1}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com