

分析 (1)根據圖形查出2張桌子,3張桌子可坐的人數,然后得出每多一張桌子可多坐2人的規律,然后解答;
(2)求出每一張大桌子可坐的人數與可拼成的大桌子數,然后相乘計算即可.
解答 解:(1)由圖可知,2張桌子拼在一起可坐8人,
3張桌子拼在一起可坐10人,
…
依此類推,每多一張桌子可多坐2人,
所以,n張桌子拼在一起可坐2n+4;
故答案為:8,10,2n+4;
(2)當n=5時,2n+4=2×5+4=14(人),
可拼成的大桌子數,45÷5=9,
14×9=116(人);
點評 此題主要考查了圖形變化規律,根據圖形,觀察得出每多一張桌子可多坐2人的規律并求出n張桌子可坐的人數的表達式是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖所示,已知△ABC中,∠BAC=90°,AB=AC,MN是經過點A的直線,BD⊥MN,CE⊥MN,垂足分別為點D、E.
如圖所示,已知△ABC中,∠BAC=90°,AB=AC,MN是經過點A的直線,BD⊥MN,CE⊥MN,垂足分別為點D、E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
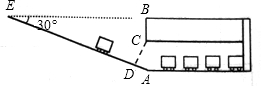 某校九年級數學興趣小組為了測得該校地下停車場的限高CD(CD⊥AE),在課外活動時間測得下列數據:如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米,試求該校地下停車場的高度AC及限高CD($\sqrt{3}$≈1.73,結果精確到0.1米)
某校九年級數學興趣小組為了測得該校地下停車場的限高CD(CD⊥AE),在課外活動時間測得下列數據:如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米,試求該校地下停車場的高度AC及限高CD($\sqrt{3}$≈1.73,結果精確到0.1米)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
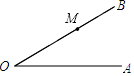 如圖,∠AOB=30°,點M在OB上,且OM=5cm,以M為圓心,r為半徑畫圓,試討論r的大小與所畫⊙M和射線OA的公共點個數之間的對應關系.
如圖,∠AOB=30°,點M在OB上,且OM=5cm,以M為圓心,r為半徑畫圓,試討論r的大小與所畫⊙M和射線OA的公共點個數之間的對應關系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
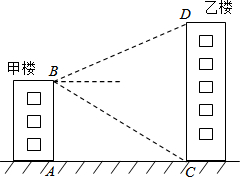 如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂的B處看乙樓樓頂的D處,仰角為28°,求乙樓的高CD的長.(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
如圖,甲、乙兩樓的距離AC=30m,甲樓高AB=40m,自甲樓樓頂的B處看乙樓樓頂的D處,仰角為28°,求乙樓的高CD的長.(結果精確到0.1m,參考數據:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com