
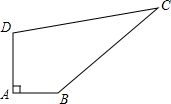
 如圖所示,四邊形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四邊形ABCD的面積.
如圖所示,四邊形ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,求四邊形ABCD的面積. 分析 如圖,連接BD.首先利用勾股定理求出BD,再利用勾股定理的逆定理證明△BDC是直角三角形,分別求出△ABD,△DBC的面積即可解決問題.
解答 解:如圖,連接BD.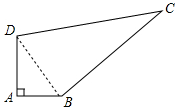
在Rt△ABD中,∵∠A=90°,AD=4,AB=3,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵BD2+BC2=52+122=169,DC2=132=169,
∴BD2+BC2=CD2,
∴△BDC是直角三角形,
∴S△DBC=$\frac{1}{2}$•BD•BC=$\frac{1}{2}$×5×12=30,S△ABD=$\frac{1}{2}$•AD•AB=$\frac{1}{2}$×3×4=6,
∴四邊形ABCD的面積=S△BDC+S△ADB=36.
點評 本題考查勾股定理、勾股定理的逆定理、三角形的面積等知識,解題的關鍵是把四邊形問題轉化為三角形問題解決,屬于中考常考題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將三個同樣的正方形的一個頂點重合放置,如果∠1=45°,∠3=30°時,那么∠2的度數是( )
如圖,將三個同樣的正方形的一個頂點重合放置,如果∠1=45°,∠3=30°時,那么∠2的度數是( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
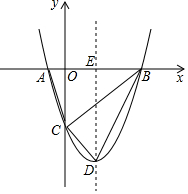 如圖,拋物線與x軸交于A,B兩點,點B坐標是(3,0),與y軸交于點C,頂點D的坐標是(1,-4),對稱軸與x軸交于點E
如圖,拋物線與x軸交于A,B兩點,點B坐標是(3,0),與y軸交于點C,頂點D的坐標是(1,-4),對稱軸與x軸交于點E查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
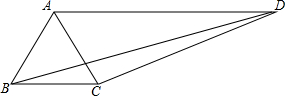 在四邊形ABCD中,連接對角線AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,則BD=3$\sqrt{13}$.
在四邊形ABCD中,連接對角線AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,則BD=3$\sqrt{13}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
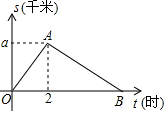 平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題
平頂山市教育局舉行'重走長征路”健步活動,某教師從起點體育村沿建設路到市生態園.再沿原路返回.該教師離開起點的路程S(千米)與步行時間t(小時)之間的函數關系如圖所示.其中從起點到市生態園的平均速度是4千米/小時.用2小時.根據圖象提供信息.解答下列問題查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com