
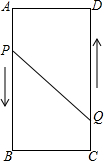
 A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.
A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.分析 (1)當PB=CQ時,四邊形PBCQ為矩形,依此建立方程求出即可;
(2)作PH⊥CD,垂足為H,設運動時間為t秒,用t表示線段長,用勾股定理列方程求解.
解答 解:(1)如圖,∵A、B、C、D為矩形的四個頂點,
∴∠B=90°,AB∥CD,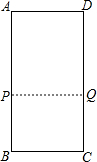
∴當PB=CQ時,四邊形PBCQ為矩形,
設P、Q兩點從出發開始到t秒時四邊形PBCQ是矩形,
則16-3t=2t,
解得:t=$\frac{16}{5}$.
答:當P、Q兩點從出發開始到$\frac{16}{5}$秒時四邊形PBCQ是矩形秒時四邊形APQD為矩形;
(2)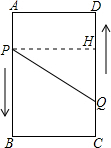 設P,Q兩點從出發開始到t秒時,點P,Q間的距離是10cm,
設P,Q兩點從出發開始到t秒時,點P,Q間的距離是10cm,
作PH⊥CD,垂足為H,則PH=AD=6,PQ=10,
∵DH=PA=3t,CQ=2t,
∴HQ=CD-DH-CQ=|16-5t|,
由勾股定理,得(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:P,Q兩點從出發開始到1.6或4.8秒時,點P,Q間的距離是10cm.
點評 本題考查了一元二次方程的應用,矩形的性質及判定,勾股定理等知識,綜合性較強,利用數形結合、分類討論及方程思想是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的算術平方根是2 | D. | $\sqrt{8}$是最簡二次根式 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
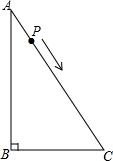 如圖,直角三角形ABC中,CB=6,AC=8,點P沿AC以每秒2個單位長度的速度從A向C運動,設點P運動時間為t秒,當t=2時,三角形BPC的面積等于三角形ABC面積的一半.
如圖,直角三角形ABC中,CB=6,AC=8,點P沿AC以每秒2個單位長度的速度從A向C運動,設點P運動時間為t秒,當t=2時,三角形BPC的面積等于三角形ABC面積的一半.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
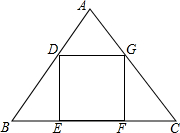 如圖,正方形DEFG的邊EF在△ABC的邊BC上,頂點D、G分別在邊AB、AC上,已知BC=6,△ABC的面積為9,則正方形DEFG的面積為4.
如圖,正方形DEFG的邊EF在△ABC的邊BC上,頂點D、G分別在邊AB、AC上,已知BC=6,△ABC的面積為9,則正方形DEFG的面積為4.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com