
分析 (1)設“等積點”坐標為(m,n),則有$\left\{\begin{array}{l}{mn=4}\\{m-n=4}\end{array}\right.$解方程組即可.
(2)如圖,由題意“等積點”在反比例函數y=$\frac{k}{x}$圖象上,直線y=-x+b(b>0)與x軸、y軸分別交于點A和點B,并且直線有且只有一個“等積點”,所以“等積點”M的坐標為($\sqrt{k}$,$\sqrt{k}$),B(0,2$\sqrt{k}$),A(2$\sqrt{k}$,0),E(2$\sqrt{K}$,$\frac{1}{2}$$\sqrt{k}$),F($\frac{1}{2}$$\sqrt{k}$,2$\sqrt{k}$),根據△OEF的面積=S正方形AOBC-2•S△AOE-S△EFC=k2+$\frac{5}{4}$k-$\frac{3}{8}$,列出方程即可解決問題.
解答 解:(1)設“等積點”坐標為(m,n),則有$\left\{\begin{array}{l}{mn=4}\\{m-n=4}\end{array}\right.$解得$\left\{\begin{array}{l}{m=2\sqrt{2}+2}\\{n=2\sqrt{2}-2}\end{array}\right.$或$\left\{\begin{array}{l}{m=2-2\sqrt{2}}\\{n=-2-2\sqrt{2}}\end{array}\right.$(舍棄),
∴“等積點”坐標為(2$\sqrt{2}$+2,2$\sqrt{2}$-2).
(2)如圖,由題意“等積點”在反比例函數y=$\frac{k}{x}$圖象上,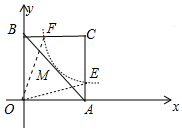
∵直線y=-x+b(b>0)與x軸、y軸分別交于點A和點B,并且直線有且只有一個“等積點”,
∴“等積點”M的坐標為($\sqrt{k}$,$\sqrt{k}$),B(0,2$\sqrt{k}$),A(2$\sqrt{k}$,0),E(2$\sqrt{K}$,$\frac{1}{2}$$\sqrt{k}$),F($\frac{1}{2}$$\sqrt{k}$,2$\sqrt{k}$),
∵△OEF的面積=S正方形AOBC-2•S△AOE-S△EFC=k2+$\frac{5}{4}$k-$\frac{3}{8}$,
∴k2+$\frac{5}{4}$k-$\frac{3}{8}$=4k-k-$\frac{9}{8}$k,
解得k=1或-$\frac{3}{8}$(舍棄),
∴E(2,$\frac{1}{2}$),F($\frac{1}{2}$,2),
∴EF=$\sqrt{(2-\frac{1}{2})^{2}+(\frac{1}{2}-2)^{2}}$=$\frac{3}{2}$$\sqrt{2}$.
點評 本題考查一次函數綜合題、反比例函數的應用、二元一次方程組等知識,解題的關鍵是靈活運用所學知識解決問題,學會利用參數解決問題,學會用方程或方程組的思想思考問題,屬于中考壓軸題.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
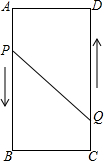 A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.
A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com