
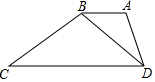
 在梯形ABCD中,AB∥CD,連結BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的長.
在梯形ABCD中,AB∥CD,連結BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的長. 分析 由AB∥CD知∠ABD=∠BDC,結合∠ADB=∠C可證△ABD∽△BDC,得$\frac{AB}{BD}=\frac{AD}{BC}=\frac{BD}{DC}$,據此可得.
解答 解:∵AB∥CD,
∴∠ABD=∠BDC,
又∵∠ADB=∠C,
∴△ABD∽△BDC,
則$\frac{AB}{BD}=\frac{AD}{BC}=\frac{BD}{DC}$,即$\frac{8}{BD}=\frac{10}{15}=\frac{BD}{DC}$,
解得:BD=12,CD=18.
點評 本題主要考查相似三角形的判定與性質及平行線的性質,在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構造相似三角形;或依據基本圖形對圖形進行分解、組合;或作輔助線構造相似三角形,判定三角形相似的方法有事可單獨使用,有時需要綜合運用,無論是單獨使用還是綜合運用,都要具備應有的條件方可.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
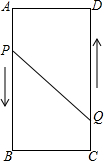 A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.
A、B、C、D為矩形的四個頂點,AB=16cm,AD=6cm,動點P、Q分別從點A、C同時出發,點P以3cm/s的速度向點B移動,一直到達B為止,點Q以2cm/s的速度向D移動.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
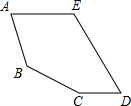 聰聰用五根寬度相同的木條拼成了一個五邊形,如圖所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.
聰聰用五根寬度相同的木條拼成了一個五邊形,如圖所示,已知AE∥CD,∠A=$\frac{1}{2}$∠C,∠B=120°,∠D=50°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1,還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2;按上述方法不斷操作下去…,經過第2015次操作后得到的折痕D2014E2014,到BC的距離記為h2015;若h1=1,則h2016的值為2-$\frac{1}{{2}^{2015}}$.
如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1處,稱為第1次操作,折痕DE到BC的距離記為h1,還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2;按上述方法不斷操作下去…,經過第2015次操作后得到的折痕D2014E2014,到BC的距離記為h2015;若h1=1,則h2016的值為2-$\frac{1}{{2}^{2015}}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com