
分析 (1)把A(2,0)代入y=mx2-nx+n-2,即可用含n的代數(shù)式表示m;
(2)只需證明△=(-n)2-4m(n-2)>0即可;
(3)①根據(jù)題意用含n的代數(shù)式表示t,可得t1-t2=$\frac{2{n}_{1}-4}{{n}_{1}+2}$-$\frac{2{n}_{2}-4}{{n}_{2}+2}$=$\frac{8({n}_{1}-{n}_{2})}{({n}_{1}+2)({n}_{2}+2)}$,依此可得t1-t2<0,從而求解;
②t=$\frac{2n-4}{n+2}$=2-$\frac{8}{n+2}$,因?yàn)閠為整數(shù)且n>0,可得n+2>2,得到n+2=4或n+2=8,解方程即可求解.
解答 解:(1)把A(2,0)代入y=mx2-nx+n-2,得4m-2n+n-2=0,m=$\frac{n+2}{4}$;
(2)∵△=(-n)2-4m(n-2)=n2-4×$\frac{n+2}{4}$×(n-2)=n2-n2+4=4>0,
∴二次函數(shù)y=mx2-nx+n-2的圖象與x軸始終有2個(gè)交點(diǎn);
(3)①依題意可知t=$\frac{2n-4}{n+2}$;
所以t1-t2=$\frac{2{n}_{1}-4}{{n}_{1}+2}$-$\frac{2{n}_{2}-4}{{n}_{2}+2}$=$\frac{8({n}_{1}-{n}_{2})}{({n}_{1}+2)({n}_{2}+2)}$,
因?yàn)閚1<n2,所以n1-n2<0,
又因?yàn)閚>0,
所以n1+2>0,n2+2>0,
所以t1-t2<0,
所以t1<t2;
②t=$\frac{2n-4}{n+2}$=2-$\frac{8}{n+2}$,
因?yàn)閠為整數(shù)且n>0,
所以n+2>2,
所以n+2=4或n+2=8
所以n=2或n=6.
點(diǎn)評(píng) 本題考查了拋物線與x軸的交點(diǎn).解答本題的關(guān)鍵是根據(jù)根的判別式△>0證明拋物線與x軸有兩個(gè)交點(diǎn).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
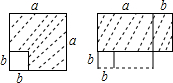 如圖,在邊長(zhǎng)為a的正方形中挖掉一個(gè)邊長(zhǎng)為b的小正方形(a>b),把余下的部分剪拼成為一個(gè)矩形,通過(guò)計(jì)算兩個(gè)圖形(陰影部分)的面積,可以驗(yàn)證的等式是( )
如圖,在邊長(zhǎng)為a的正方形中挖掉一個(gè)邊長(zhǎng)為b的小正方形(a>b),把余下的部分剪拼成為一個(gè)矩形,通過(guò)計(jì)算兩個(gè)圖形(陰影部分)的面積,可以驗(yàn)證的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的算術(shù)平方根是2 | D. | $\sqrt{8}$是最簡(jiǎn)二次根式 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,把拋物線y=$\frac{1}{2}$x2平移得到拋物線m,拋物線m經(jīng)過(guò)點(diǎn)A(-8,0)和原點(diǎn)O(0,0),它的頂點(diǎn)為P,它的對(duì)稱軸與拋物線y=$\frac{1}{2}$x2交于點(diǎn)Q,則圖中陰影部分的面積為32.
如圖,把拋物線y=$\frac{1}{2}$x2平移得到拋物線m,拋物線m經(jīng)過(guò)點(diǎn)A(-8,0)和原點(diǎn)O(0,0),它的頂點(diǎn)為P,它的對(duì)稱軸與拋物線y=$\frac{1}{2}$x2交于點(diǎn)Q,則圖中陰影部分的面積為32.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
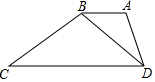 在梯形ABCD中,AB∥CD,連結(jié)BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的長(zhǎng).
在梯形ABCD中,AB∥CD,連結(jié)BD,且∠ADB=∠C,又AB=8,BC=15,AD=10,求CD的長(zhǎng).查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com