
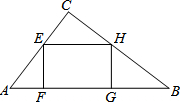
 如圖,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,點E在邊AC上,過點E作EF⊥AB交AB于點F,EH∥AB交BC于點H,邊點H作HG⊥AB于點G,設EF=x.
如圖,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,點E在邊AC上,過點E作EF⊥AB交AB于點F,EH∥AB交BC于點H,邊點H作HG⊥AB于點G,設EF=x.分析 (1)由△AFE∽△ACB,推出$\frac{AE}{AB}$=$\frac{EF}{BC}$=$\frac{AF}{AC}$,推出$\frac{AE}{10}$=$\frac{x}{8}$=$\frac{AF}{6}$,推出AE=$\frac{5}{4}$x,AF=$\frac{3}{4}$x,EC=6-$\frac{5}{4}$x,由△AEF與△CEH全等,∠A=∠CEH,推出EC=AF,可得6-$\frac{5}{4}$x=$\frac{3}{4}$x,解方程即可.
(2)以FG為直徑作⊙O,作OM⊥EH于M.當OM≤OF時,EH上存在點P,使得∠FPG=90°,列出不等式即可解決問題.
解答 解:(1)在Rt△ABC中,∵BC=10,sinB=$\frac{3}{5}$,
∴AC=6,BC=8,
∵∠A=∠A.∠AFE=∠C=90°,
∴△AFE∽△ACB,
∴$\frac{AE}{AB}$=$\frac{EF}{BC}$=$\frac{AF}{AC}$,
∴$\frac{AE}{10}$=$\frac{x}{8}$=$\frac{AF}{6}$,
∴AE=$\frac{5}{4}$x,AF=$\frac{3}{4}$x,EC=6-$\frac{5}{4}$x,
∵△AEF與△CEH全等,∠A=∠CEH,
∴EC=AF,
∴6-$\frac{5}{4}$x=$\frac{3}{4}$x,
∴x=3.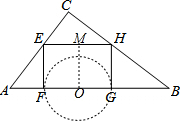
(2)以FG為直徑作⊙O,作OM⊥EH于M.
當OM≤OF時,EH上存在點P,使得∠FPG=90°,
∵△CEH∽△CAB,
∴$\frac{CE}{CA}$=$\frac{EH}{AB}$,
∴EH=$\frac{5}{3}$(6-$\frac{5}{4}$x),
∴x≤$\frac{1}{2}$($\frac{5}{3}$(6-$\frac{5}{4}$x),
∴x≤$\frac{120}{49}$,∵x>0,
∴0<x≤$\frac{120}{49}$.
點評 本題考查相似三角形的判定和性質、矩形的性質、解直角三角形、圓的有關知識,解題的關鍵是學會用方程的思想思考問題,學會利用輔助圓解決直角問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
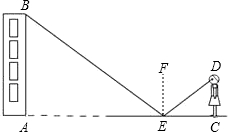 小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角)
小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
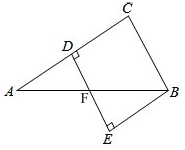 如圖,△ABC中,AC的中垂線交AC、AB于點D、F,BE⊥DF交DF延長線于點E,若∠A=30°,BC=6,AF=BF,則四邊形BCDE的面積是18$\sqrt{3}$.
如圖,△ABC中,AC的中垂線交AC、AB于點D、F,BE⊥DF交DF延長線于點E,若∠A=30°,BC=6,AF=BF,則四邊形BCDE的面積是18$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{a}^{2016}}{2015}$ | B. | $\frac{{a}^{2016}}{2016}$ | C. | $\frac{{a}^{4030}}{2015}$ | D. | $\frac{{a}^{4032}}{2016}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com