
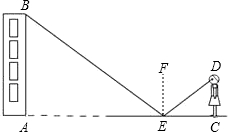
 小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角)
小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角) 分析 根據反射角等于入射角可得∠AEB=∠CED,則可判斷Rt△AEB∽Rt△CED,根據相似三角形的性質得$\frac{AB}{1.6}$=$\frac{21}{2.5}$,然后利用比例性質求出AB即可.
解答 解:根據題意得∠AEB=∠CED,
∵Rt△AEB∽Rt△CED,
∴$\frac{AB}{CD}$=$\frac{AE}{CE}$,即$\frac{AB}{1.6}$=$\frac{21}{2.5}$,
解得:AB=13.44.
答:教學樓的高度為13.44m.
點評 本題考查了相似三角形的應用:利用入射與反射構造相似三角形,然后利用相似三角形的性質即相似三角形的對應邊的比相等解決問題.


科目:初中數學 來源: 題型:解答題
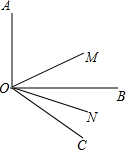 如圖,OB是∠AOC內的一條射線,OM平分∠AOC,ON平分∠BOC,其中∠BOC是銳角.
如圖,OB是∠AOC內的一條射線,OM平分∠AOC,ON平分∠BOC,其中∠BOC是銳角.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,將長方形ABCD沿AE折疊,使點D落在BC邊上的點F,若∠BAF=60°,則∠DAE=( )
如圖,將長方形ABCD沿AE折疊,使點D落在BC邊上的點F,若∠BAF=60°,則∠DAE=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
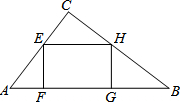 如圖,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,點E在邊AC上,過點E作EF⊥AB交AB于點F,EH∥AB交BC于點H,邊點H作HG⊥AB于點G,設EF=x.
如圖,在Rt△ABC中,∠ACB=90°,AB=10,sinB=$\frac{3}{5}$,點E在邊AC上,過點E作EF⊥AB交AB于點F,EH∥AB交BC于點H,邊點H作HG⊥AB于點G,設EF=x.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com