
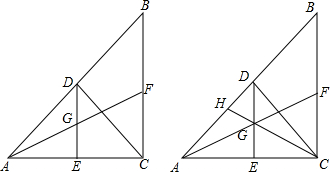
分析 (1)由直角三角形的性質得出∠BAC=∠DCB,由AAS證明△ADE≌△CBD,即可得出∴DE=DB;
(2)證出DE∥BC,由平行線分線段成比例定理得出$\frac{DG}{BF}=\frac{AG}{AF}$,$\frac{AG}{AF}=\frac{GE}{FC}$,證出$\frac{DG}{BF}=\frac{GE}{FC}$,再由已知條件即可得出結論;
(3)連接HF,過H作HM⊥AC于M,連接DM,如圖所示:由平行線證出AM=CM=$\frac{1}{2}$AC=2,得出DM=$\frac{1}{2}$AC=2,由三角形中位線定理得出HF∥AC,HF=$\frac{1}{2}$AC,由平行線得出比例式$\frac{AG}{GF}=\frac{AC}{HF}$=2,求出AE=$\frac{2}{3}$AC=$\frac{8}{3}$,得出ME=AE-AM=$\frac{2}{3}$,在Rt△DEM中,由勾股定理求出DE即可.
解答 (1)證明:∵∠ACB=90°,
∴∠B+∠BAC=90°,
∵CD為AB邊上的高線,
∴∠CDB=90°,
∴∠DCB+∠B=90°,
∴∠BAC=∠DCB,
∵DE⊥AC,
∴∠DEA=∠CDB=90°,
在△ADE和△CBD中,$\left\{\begin{array}{l}{∠DAE=∠DCB}&{\;}\\{∠DEA=∠CDB}&{\;}\\{AD=CB}&{\;}\end{array}\right.$,
∴△ADE≌△CBD(AAS),
∴DE=DB;
(2)證明:∵∠ACB=90°,
∴BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴$\frac{DG}{BF}=\frac{AG}{AF}$,$\frac{AG}{AF}=\frac{GE}{FC}$,
∴$\frac{DG}{BF}=\frac{GE}{FC}$,
∵G是DE的中點,
∴DG=GE,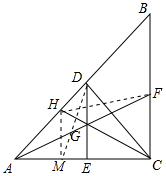
∴BF=FC,
∴F是BC的中點;
(3)解:連接HF,過H作HM⊥AC于M,連接DM,如圖所示:
∵HM⊥AC,BC⊥AC,
∴HM∥BC,
∵AH=BH,
∴AM=CM=$\frac{1}{2}$AC=2,
∵CD⊥AB,
∴△ADC是直角三角形,
∴DM=$\frac{1}{2}$AC=2,
∵F是BC中點,
∴HF∥AC,HF=$\frac{1}{2}$AC,
∴$\frac{AG}{GF}=\frac{AC}{HF}$=2,
∴$\frac{AG}{AF}=\frac{AE}{AC}$=$\frac{2}{3}$,
∴AE=$\frac{2}{3}$AC=$\frac{8}{3}$,
∴ME=AE-AM=$\frac{8}{3}$-2=$\frac{2}{3}$,
在Rt△DEM中,DE=$\sqrt{D{M}^{2}-M{E}^{2}}$=$\sqrt{{2}^{2}-(\frac{2}{3})^{2}}$=$\frac{4}{3}$$\sqrt{2}$.
點評 本題是三角形綜合題目,考查了全等三角形的判定與性質、平行線的判定、平行線分線段成比例定理、等腰三角形的判定與性質、三角形中位線定理、勾股定理等知識;本題綜合性強,有一定難度.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x(x+8)=9 | B. | x(8-x)=9 | C. | x(16-x)=9 | D. | x(16-2x)=9 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖、正比例函數y1=k1x與反比例函數y2=$\frac{{k}_{2}}{x}$的圖象交于(1,2),則在第一象限內不等式k1x>$\frac{{k}_{2}}{x}$的解集為x>1.
如圖、正比例函數y1=k1x與反比例函數y2=$\frac{{k}_{2}}{x}$的圖象交于(1,2),則在第一象限內不等式k1x>$\frac{{k}_{2}}{x}$的解集為x>1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
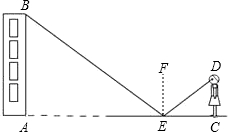 小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角)
小強在地面E處放一面鏡子,剛好能從鏡子中看到教學樓的頂端B,此時EA=21米,CE=2.5米.已知眼睛距離地面的高度DC=1.6米,請計算出教學樓的高度.(根據光的反射定律,反射角等于入射角)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com