
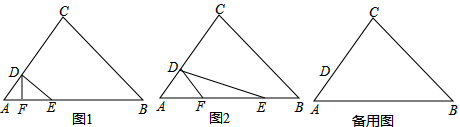
分析 (1)根據三角形的面積得到CH的值,根據勾股定理得到AH,然后根據三角函數的定義即可得到結論;
(2)過點D作DG⊥AB,交AB于G,先證出△EDF∽△EAD,得出ED2=AE•EF,再求出DG、AG,最后根據EG=x-3,DE2=42+(x-3)2得出42+(x-3)2=x•(x-y),
再進行整理即可;
(3)先證出∠AFD=∠EDC,再分兩種情況討論:①當∠A=∠CED時,得出$\frac{AD}{AC}$=$\frac{AF}{AE}$,$\frac{5}{25}$=$\frac{y}{x}$,再把y=6-$\frac{25}{x}$代入得出5(6-$\frac{25}{x}$)=x,再解方程即可;②當∠A=∠DCE時,根據△ECD∽△DAF得出$\frac{CD}{AF}$=$\frac{CE}{AD}$,$\frac{20}{y}$=$\frac{x}{5}$,再把y=6-$\frac{25}{x}$代入得出5(6-$\frac{25}{x}$)=x,求出方程的解即可.
解答 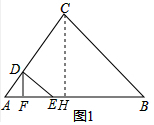 解:(1)如圖1,∵CH⊥AB,AB=35,S△ABC=350,
解:(1)如圖1,∵CH⊥AB,AB=35,S△ABC=350,
∴S△ABC=$\frac{1}{2}$AB•CH=350,
∴CH=20,
∴AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=15,
∴tan A=$\frac{CH}{AH}$=$\frac{20}{15}$=$\frac{4}{3}$,
故答案為:20,$\frac{4}{3}$;
(2)如圖2,過點D作DG⊥AB,交AB于G,
∵∠EDF=∠EAD,∠DEF=∠AED,
∴△EDF∽△EAD,
∴$\frac{ED}{EF}$=$\frac{AE}{ED}$,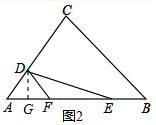
∴ED2=AE•EF,
∴RT△AGD中,∠AGD=90°,AD=5,tanA=$\frac{4}{3}$,
∴DG=4,AG=3,
∴EG=x-3,
∴DE2=42+(x-3)2,
∴42+(x-3)2=x•(x-y),
∴y=6-$\frac{25}{x}$ ($\frac{25}{6}$≤x≤35);
(3)∵∠A+∠AFD=∠EDF+∠EDC,且∠EDF=∠A,
∴∠AFD=∠EDC,
①當∠A=∠CED時,
∵∠EDF=∠A,
又∵∠CED=∠FDE,
∴DF∥CE
∴$\frac{AD}{AC}$=$\frac{AF}{AE}$,∴$\frac{5}{25}$=$\frac{y}{x}$,
∵y=6-$\frac{25}{x}$,
∴5(6-$\frac{25}{x}$)=x,
x1=25,x2=5;
②當∠A=∠DCE時,
∵∠EDF=∠A,
∴△ECD∽△DAF
∴$\frac{CD}{AF}$=$\frac{CE}{AD}$,
∴$\frac{20}{y}$=$\frac{x}{5}$,
∵y=6-$\frac{25}{x}$,
∴5(6-$\frac{25}{x}$)=x,
∴x=$\frac{125}{6}$,
∴當△DEC和△ADF相似時,x=25或x=5或x=$\frac{125}{6}$.
點評 此題考查了相似形的綜合,用到的知識點是相似三角形的判定與性質、勾股定理、銳角三角函數,關鍵是根據題意作出輔助線,構造相似三角形.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{x-3}{x}$ | B. | $\frac{x+3}{x}$ | C. | $\frac{x}{x-3}$ | D. | $\frac{x}{x+3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
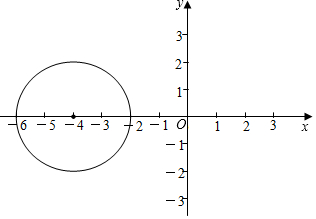 如圖,在平面直角坐標系中,點P的坐標為(-4,0),⊙P的半徑為2,將⊙P沿x軸向右平移4個單位長度得
如圖,在平面直角坐標系中,點P的坐標為(-4,0),⊙P的半徑為2,將⊙P沿x軸向右平移4個單位長度得查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com