
如圖,在平面直角坐標系中,一拋物線的對稱軸為直線 ,與y軸負半軸交于C點,與x軸交于A、B兩點,其中B點的坐標為(3,0),且OB=OC.
,與y軸負半軸交于C點,與x軸交于A、B兩點,其中B點的坐標為(3,0),且OB=OC.

(1)求此拋物線的解析式;
(2)若點G(2,y)是該拋物線上一點,點P是直線AG下方的拋物線上一動點,當點P運動到什么位置時,△APG的面積最大?求出此時P點的坐標和△APG的最大面積.
(3)若平行于x軸的直線與該拋物線交于M、N兩點(其中點M在點N的右側(cè)),在x軸上是否存在點Q,使△MNQ為等腰直角三角形?若存在,請求出點Q的坐標;若不存在,請說明理由.
(1)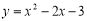 ;(2)P點的坐標為
;(2)P點的坐標為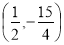 ,
,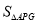 的最大值為
的最大值為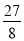 ;(3)Q(-
;(3)Q(-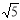 ,0)或(
,0)或(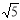 ,0)或(
,0)或(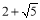 ,0)或(
,0)或(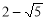 ,0)或(1,0).
,0)或(1,0).
【解析】
試題分析:(1)設(shè)拋物線的解析式為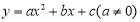 ,根據(jù)已知得到C(0,﹣3),A(﹣1,0),代入得到方程組
,根據(jù)已知得到C(0,﹣3),A(﹣1,0),代入得到方程組 ,求出方程組的解即可;
,求出方程組的解即可;
(2)過點P作y軸的平行線與AG交于點F,求出點G的坐標(2,﹣3),設(shè)直線AG為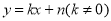 ,代入得到
,代入得到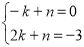 ,求出方程組的解得出直線AG為
,求出方程組的解得出直線AG為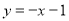 ,設(shè)P(x,
,設(shè)P(x,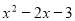 ),則F(x,﹣x﹣1),PF
),則F(x,﹣x﹣1),PF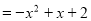 ,根據(jù)三角形的面積公式求出△APG的面積,化成頂點式即可;
,根據(jù)三角形的面積公式求出△APG的面積,化成頂點式即可;
(3)存在.根據(jù)MN∥x軸,且M、N在拋物線上,得到M、N關(guān)于直線x=1對稱,設(shè)點M為(m,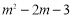 )且m>1,得到MN=2(m﹣1),當∠QMN=90°,且MN=MQ時,由△MNQ為等腰直角三角形,得到
)且m>1,得到MN=2(m﹣1),當∠QMN=90°,且MN=MQ時,由△MNQ為等腰直角三角形,得到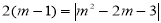 ,求出m的值,得出點M和點Q的坐標;當∠QNM=90°,且MN=NQ時,同理可求點Q的坐標,當∠NQM=90°,且MQ=NQ時,過Q作QE⊥MN于點E,則QE=
,求出m的值,得出點M和點Q的坐標;當∠QNM=90°,且MN=NQ時,同理可求點Q的坐標,當∠NQM=90°,且MQ=NQ時,過Q作QE⊥MN于點E,則QE=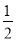 MN,根據(jù)拋物線及等腰直角三角形的軸對稱性,得到點Q的坐標.
MN,根據(jù)拋物線及等腰直角三角形的軸對稱性,得到點Q的坐標.
試題解析:(1)設(shè)拋物線的解析式為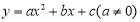 ,
,
由已知得:C(0,﹣3),A(﹣1,0),
∴ ,解得
,解得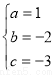 ,
,
∴拋物線的解析式為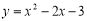 ;
;
(2)過點P作y軸的平行線與AG交于點Q,
由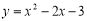 ,令x=2,則y=-3,∴點G為(2,-3),
,令x=2,則y=-3,∴點G為(2,-3),
設(shè)直線AG為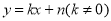 ,∴
,∴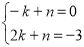 ,解得:
,解得: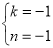 ,即直線AG為
,即直線AG為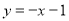 ,
,
設(shè)P(x,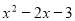 ),則F(x,-x-1),PF
),則F(x,-x-1),PF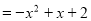 .
.
∵ ,
,
∴當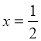 時,△APG的面積最大,此時P點的坐標為
時,△APG的面積最大,此時P點的坐標為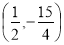 ,
,
(3)存在.
∵MN∥x軸,且M、N在拋物線上,∴M、N關(guān)于直線x=1對稱,
設(shè)點M為(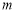 ,
,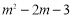 )且
)且 ,∴
,∴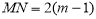 ,
,
當∠QMN=90°,且MN=MQ時,△MNQ為等腰直角三角形,∴MQ⊥MN即MQ⊥x軸,
∴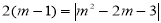 ,即
,即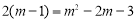 或
或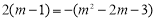 ,
,
解得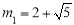 ,
,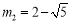 (舍)或
(舍)或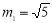 ,
,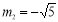 (舍),
(舍),
∴點M為(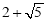 ,
,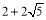 )或(
)或(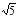 ,
,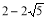 ),∴點Q為(
),∴點Q為(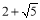 ,0)或(
,0)或(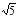 ,0),
,0),
當∠QNM=90°,且MN=NQ時,△MNQ為等腰直角三角形,同理可求點Q為(-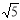 ,0)或(
,0)或(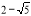 ,0),
,0),
當∠NQM=90°,且MQ=NQ時,△MNQ為等腰直角三角形,
過Q作QE⊥MN于點E,則QE=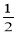 MN,
MN,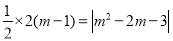 ,
,
∵方程有解,∴由拋物線及等腰直角三角形的軸對稱性知點Q為(1,0),
綜上所述,滿足存在滿足條件的點Q,分別為(-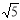 ,0)或(
,0)或(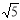 ,0)或(
,0)或(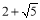 ,0)或(
,0)或(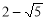 ,0)或(1,0).
,0)或(1,0).
考點:1.二次函數(shù)綜合題;2.等腰直角三角形.


科目:初中數(shù)學 來源:2014-2015學年遼寧省莊河市九年級上學期第一次月考數(shù)學試卷(解析版) 題型:填空題
關(guān)于x的一元二次方程 沒有實數(shù)根,則k的取值范圍是
沒有實數(shù)根,則k的取值范圍是
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市九年級上學期期中考試數(shù)學試卷(解析版) 題型:選擇題
如圖,已知AB∥CD,直線EF分別交AB、CD于點E、F,EG平分∠BEF,若∠1=50°,則∠2的度數(shù)是( )

A.70° B.65° C.60° D.50°
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市等九年級模擬聯(lián)考數(shù)學試卷(解析版) 題型:選擇題
如圖,在□ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分線分別交AD于E和F,BE與CF交于點G,則△EFG與△BCG面積之比是( )
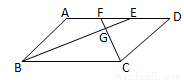
A.5:8 B.25:64 C.1:4 D.1:16
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市等九年級模擬聯(lián)考數(shù)學試卷(解析版) 題型:解答題
某校學生會準備調(diào)查初中2010級同學每天(除課間操外)的課外鍛煉時間.

(1)確定調(diào)查方式時,甲同學說:“我到1班去調(diào)查全體同學”;乙同學說:“我到體育場上去詢問參加鍛煉的同學”;丙同學說:“我到初中2010級每個班去隨機調(diào)查一定數(shù)量的同學”.請你指出哪位同學的調(diào)查方式最為合理;
(2)他們采用了最為合理的調(diào)查方法收集數(shù)據(jù),并繪制出如圖-1所示的條形統(tǒng)計圖和如圖-2所示的扇形統(tǒng)計圖,則他們共調(diào)查了多少名學生?請將兩個統(tǒng)計圖補充完整;
(3)若該校初中2010級共有240名同學,請你估計該年級每天(除課間操外)課外鍛煉時間不大于20分鐘的人數(shù).
(注:圖-2中相鄰兩虛線形成的圓心角為30°.)
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市等九年級模擬聯(lián)考數(shù)學試卷(解析版) 題型:填空題
為了了解貫徹執(zhí)行國家提倡的“陽光體育運動”的實施情況,將某班50名同學一周的體育鍛煉情況繪制成了如圖所示的條形統(tǒng)計圖,根據(jù)統(tǒng)計圖提供的數(shù)據(jù),該班50名同學一周參加體育鍛煉時間的中位數(shù)與眾數(shù)之和為 .

查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市等五校九年級上學期期中聯(lián)考數(shù)學試卷(解析版) 題型:選擇題
如圖,是由相同的花盆按一定的規(guī)律組成的形如正多邊形的圖案,其中第1個圖形一共有6個花盆,第2個圖形一共有12個花盆,第3個圖形一共有20個花盆,…則第8個圖形中花盆的個數(shù)為( )

A.56 B.64 C.72 D.90
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年重慶市校七年級12月月考數(shù)學試卷(解析版) 題型:選擇題
如圖,將一副三角尺按不同位置擺放,擺放方式中∠ 與∠
與∠ 互余的是( )
互余的是( )

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com