
分析 (1)①由對稱軸是直線x=1,得到-$\frac{-(a+1)}{a}$=1,于是得到結(jié)論;②∵二次函數(shù)y=$\frac{1}{2}$x2-$\frac{3}{2}$x-t(t為實(shí)數(shù))圖象的頂點(diǎn)在x軸上,列方程得到t=-$\frac{9}{8}$;
(2)由y=ax2-ax-x向上平移1個(gè)單位得到新的拋物線k2,得到新的拋物線k2的解析式為y=ax2-ax-x+1,解方程得到x1=1,x2=$\frac{1}{a}$,于是得到結(jié)論.
解答 解:(1)①∵對稱軸是直線x=1,
∴-$\frac{-(a+1)}{a}$=1,
∴a=$\frac{1}{2}$,
∴二次函數(shù)的解析式為:y=$\frac{1}{2}$x2-$\frac{3}{2}$x;
②∵二次函數(shù)y=$\frac{1}{2}$x2-$\frac{3}{2}$x-t(t為實(shí)數(shù))圖象的頂點(diǎn)在x軸上,
∴(-$\frac{3}{2}$)2+4×$\frac{1}{2}$t=0,
∴t=-$\frac{9}{8}$;
(2)∵y=ax2-ax-x向上平移1個(gè)單位得到新的拋物線k2,
∴新的拋物線k2的解析式為y=ax2-ax-x+1,
∴當(dāng)y=0時(shí),ax2-ax-x+1=0,
解得:x1=1,x2=$\frac{1}{a}$,
∴k2落在x軸上方的部分對應(yīng)的x的取值范圍:$\frac{1}{a}$<x<1.
點(diǎn)評(píng) 本題考查了拋物線與x軸的交點(diǎn),二次函數(shù)的圖象與幾何變換,求二次函數(shù)的解析式,正確的理解題意是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
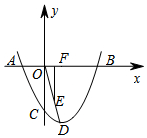 如圖,一拋物線經(jīng)過點(diǎn)A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點(diǎn),過OD的中點(diǎn)E,作EF⊥x軸于點(diǎn)F,G為x軸上一動(dòng)點(diǎn),M為拋物線上一動(dòng)點(diǎn),N為直線EF上一動(dòng)點(diǎn),當(dāng)以F、G、M、N為頂點(diǎn)的四邊形是正方形時(shí),點(diǎn)G的坐標(biāo)為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如圖,一拋物線經(jīng)過點(diǎn)A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點(diǎn),過OD的中點(diǎn)E,作EF⊥x軸于點(diǎn)F,G為x軸上一動(dòng)點(diǎn),M為拋物線上一動(dòng)點(diǎn),N為直線EF上一動(dòng)點(diǎn),當(dāng)以F、G、M、N為頂點(diǎn)的四邊形是正方形時(shí),點(diǎn)G的坐標(biāo)為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
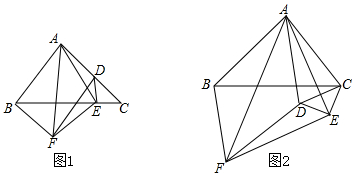
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com