
分析 存在.作DM⊥AB于M.首先證明,△ADB,△DBC的是等邊三角形,推出BD=BC=AD=$\sqrt{2}$,以B為圓心BC畫圓交AB于P,此時∠DPC=$\frac{1}{2}$∠DBC=45°,推出PB=BC=$\sqrt{2}$,由此即可解決問題.
解答 解:存在.理由如下,
如圖,作DM⊥AB于M.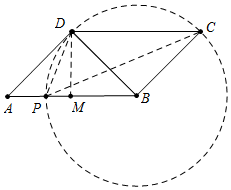
在Rt△ADM中,∵AD=$\sqrt{2}$,∠A=45°,
∴AM=DM=1,
∵AB=2,
∴AM=BM=DM=1,
∴∠ADB=90°,
∵AD∥CB,
∴∠DBC=∠ADB=90°,△ADB,△DBC的是等腰直角三角形,
∴BD=BC=AD=$\sqrt{2}$,
以B為圓心BC畫圓交AB于P,此時∠DPC=$\frac{1}{2}$∠DBC=45°,
∴PB=BC=$\sqrt{2}$,
∴AP=AB-PB=2-$\sqrt{2}$,
點評 本題考查平行四邊形的性質,圓周角定理、等腰直角三角形的判定和性質、勾股定理等知識,解題的關鍵是學會添加常用輔助線,構造輔助圓解決問題,屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,方格紙中每個小正方形的邊長都是1,△ABC的三個頂點都在格點上,如果用(1,0)表示C點的位置,用(4,1)表示B點的位置,那么.
如圖,方格紙中每個小正方形的邊長都是1,△ABC的三個頂點都在格點上,如果用(1,0)表示C點的位置,用(4,1)表示B點的位置,那么.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
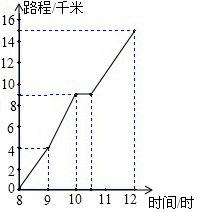 如圖為一位旅行者在早晨8時從城市出發到郊外所走的路程S(單位:千米)與時間t(單位:時)的變量關系的圖象.根據圖象回答問題:
如圖為一位旅行者在早晨8時從城市出發到郊外所走的路程S(單位:千米)與時間t(單位:時)的變量關系的圖象.根據圖象回答問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (5,2) | B. | (5,3) | C. | (6,2) | D. | (6,5) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
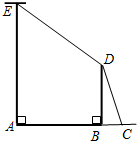 如圖,AE是位于公路邊的電線桿,高為10米,為了使電線CDE不影響汽車的正常行駛,電力部門在公路的另一邊豎立了一根水泥撐桿BD,用于撐起電線.已知兩桿之間的距離是8米,電線DE的長度為10米,求水泥撐桿BD的高度(電線桿、水泥桿的粗細忽略不計).
如圖,AE是位于公路邊的電線桿,高為10米,為了使電線CDE不影響汽車的正常行駛,電力部門在公路的另一邊豎立了一根水泥撐桿BD,用于撐起電線.已知兩桿之間的距離是8米,電線DE的長度為10米,求水泥撐桿BD的高度(電線桿、水泥桿的粗細忽略不計).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com