
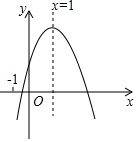 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列五個結論:
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列五個結論:分析 首先根據開口方向確定a的取值范圍,根據對稱軸的位置確定b的取值范圍,根據拋物線與y軸的交點確定c的取值范圍,判斷①;令x=-1時,代入二次函數解析式,可判斷②;當x=2時,代入二次函數解析式,可判斷③;由對稱軸x=1=-$\frac{b}{2a}$,可得a=$-\frac{b}{2}$,代入②的結論,可判斷④;根據拋物線的對稱軸為直線x=1,開口向下,得到當x=1時,y有最大值,所以am2+bm+c<a+b+c(m≠1),整理得到m(am+b)<a+b(m≠1),則可對⑤進行判斷.
解答 解:∵拋物線開口向下,
∴a<0,
∵對稱軸x=1=-$\frac{b}{2a}$,
∴b>0,
∵拋物線與y軸的交點在x軸的上方,
∴c>0,
∴abc<0,故①錯誤;
根據圖象知道當x=-1時,y=a-b+c<0,
∴a+c<b,故②錯誤;
根據圖象知道當x=2時,y=4a+2b+c>0,故③正確;
∵對稱軸x=1=-$\frac{b}{2a}$,
∴a=$-\frac{b}{2}$,
由②得b>a+c,
∴b>-$\frac{b}{2}$+c,
∴3b>2c
故④正確;
∵由圖象知,拋物線的對稱軸為直線x=1,開口向下,
∴當x=1時,y有最大值,
∴am2+bm+c<a+b+c(m≠1),
整理得到m(am+b)<a+b(m≠1),
故⑤正確;
故答案為:③④⑤.
點評 此題主要考查圖象與二次函數系數之間的關系,會利用對稱軸的范圍求2a與b的關系,以及二次函數與方程之間的轉換是解答此題的關鍵.


科目:初中數學 來源: 題型:解答題
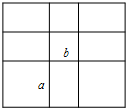 用2個邊長為a cm的大正方形,2個邊長為b cm的小正方形,5個長、寬分別為a cm、b cm的全等小長方形拼成了如圖所示的大長方形.若4個正方形的面積和為68cm2,1個小長方形的面積為15cm2,求這個大長方形的周長.
用2個邊長為a cm的大正方形,2個邊長為b cm的小正方形,5個長、寬分別為a cm、b cm的全等小長方形拼成了如圖所示的大長方形.若4個正方形的面積和為68cm2,1個小長方形的面積為15cm2,求這個大長方形的周長.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -1<k<0 | B. | -4<k<0 | C. | 0<k<1 | D. | 0<k<4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com