
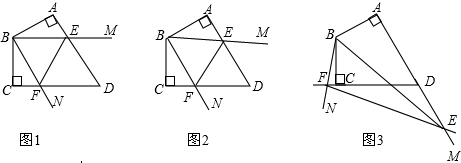
分析 延長DC至點K,使CK=AE,連接BK,則△BAE≌△BCK,然后可得BE=BK,∠ABE=∠KBC,再證明△KBF≌△EBF,可知KF=EF,所以KC+CF=EF,即AE+CF=EF.
解答 解:圖2成立,圖3不成立.
證明圖2.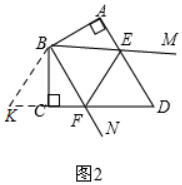
延長DC至點K,使CK=AE,連接BK,
在△BAE與△BCK中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BAE=∠BCk}\\{AE=CK}\end{array}\right.$
∴△BAE≌△BCK(SAS),
∴BE=BK,∠ABE=∠KBC,
∵∠FBE=60°,∠ABC=120°,
∴∠FBC+∠ABE=60°,
∴∠FBC+∠KBC=60°,
∴∠KBF=∠FBE=60°,
在△KBF與△EBF中
$\left\{\begin{array}{l}{BK=BE}\\{∠KBF=∠ABF}\\{BF=BF}\end{array}\right.$
∴△KBF≌△EBF(SAS),
∴KF=EF,
∴KC+CF=EF,
即AE+CF=EF.
圖3不成立,同理可證:AE、CF、EF的關系是AE-CF=EF.
點評 本題考查全等三角形的判定與性質,涉及分類討論的思想,題目較為綜合.


 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:填空題
 閱讀下面材料:在數學課上,老師請同學思考如下問題:
閱讀下面材料:在數學課上,老師請同學思考如下問題:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
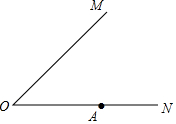 已知:如圖,∠MON及邊ON上一點A.在∠MON內部求作:點P,使得PA⊥ON,且點P 到∠MON兩邊的距離相等.(請用尺規作圖,保留作圖痕跡,不要求寫出作法,不必證明).
已知:如圖,∠MON及邊ON上一點A.在∠MON內部求作:點P,使得PA⊥ON,且點P 到∠MON兩邊的距離相等.(請用尺規作圖,保留作圖痕跡,不要求寫出作法,不必證明).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | k=4a | B. | k=-4a | C. | k=-$\frac{a}{4}$ | D. | k=4a或k=-4a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com