
 ��D��ʾ����֪��߅��ABC�ăɂ���c�����˞�A��-4��0����B��2��0����
��D��ʾ����֪��߅��ABC�ăɂ���c�����˞�A��-4��0����B��2��0�������� ��1����CH��AB��H������(j��)�cA��B�����ˣ���AB=6������(j��)���������ε�������һ�����|(zh��)����AH=BH=3���ٸ���(j��)���ɶ������CH=3$\sqrt{3}$���Ķ������cC�����ˣ�
��2������(j��)�����ε���e��ʽ�M��Ӌ�㣮
��� 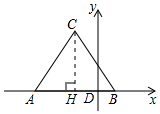 �⣺��1����CH��AB��H��
�⣺��1����CH��AB��H��
��A��-4��0����B��2��0����
��AB=6��
�ߡ�ABC�ǵ�߅�����Σ�
��AH=BH=3��
����(j��)���ɶ�������CH=3$\sqrt{3}$����C��-1��3$\sqrt{3}$����ͬ�������cC�ڵ������ޕr��C��-1��-3$\sqrt{3}$����
��C�c���˞飺C��-1��3$\sqrt{3}$����-1��-3$\sqrt{3}$����
��2��S��ABC=$\frac{1}{2}$��6��3$\sqrt{3}$=9$\sqrt{3}$��
�c�u ���}�����˵�߅�����ε����|(zh��)���ɶ������쾚�\�������ε���e��ʽ��x�S�σ��c�g�ľ��x���ڃ��c�ęM���˵IJ�Ľ^��ֵ��


 ��x��܇ϵ�д�
��x��܇ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
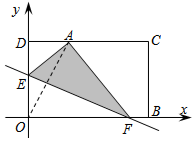 ��D����ƽ��ֱ������ϵ�У�һ�����μ�ƬOBCD���D��ʾ���ã���֪OB=10��BC=6�����@����Ƭ�ۯB��ʹ�cO����CD�ϣ�ӛ���cA���ۺ��c߅OD�����cE���c߅OB�����cF����֪�cE�����˞飨0��4�����t�cA�����˞飨2$\sqrt{3}$��6����
��D����ƽ��ֱ������ϵ�У�һ�����μ�ƬOBCD���D��ʾ���ã���֪OB=10��BC=6�����@����Ƭ�ۯB��ʹ�cO����CD�ϣ�ӛ���cA���ۺ��c߅OD�����cE���c߅OB�����cF����֪�cE�����˞飨0��4�����t�cA�����˞飨2$\sqrt{3}$��6�����鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ��x���}
| A�� | $-\frac{7}{8}$$��-\frac{5}{6}$$��-\frac{3}{4}$ | B�� | $-\frac{7}{8}$$��-\frac{3}{4}$$��-\frac{5}{6}$ | C�� | $-\frac{5}{6}$$��-\frac{7}{8}$$��-\frac{3}{4}$ | D�� | $-\frac{3}{4}$$��-\frac{5}{6}$$��-\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
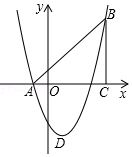 ��D����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB=90��AC=BC��OA=1��OC=4�����タy=x2+bx+c��(j��ng)�^A��B���c�����タ����c��D��
��D����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB=90��AC=BC��OA=1��OC=4�����タy=x2+bx+c��(j��ng)�^A��B���c�����タ����c��D���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
 С�A�Ͱְ���ɽ���棬�ְֳ���|܇��С�A���У�������s��ɽ�?sh��)��|܇�K�c���ϣ���֪С�A���ߵ��|܇�K�c��·���ǰְֳ��|܇��ɽ�?sh��)ľ�·�L��2�����ְ���С�A���l(f��)��50min�ų�����|܇����|܇��ƽ���ٶȞ�180m/min���O(sh��)С�A���l(f��)x��min�����ߵ�·�̞�y��m�����D�е��۾���ʾС�A�����������^����y��m���cx��min��֮�g�ĺ���(sh��)�P(gu��n)ϵ��
С�A�Ͱְ���ɽ���棬�ְֳ���|܇��С�A���У�������s��ɽ�?sh��)��|܇�K�c���ϣ���֪С�A���ߵ��|܇�K�c��·���ǰְֳ��|܇��ɽ�?sh��)ľ�·�L��2�����ְ���С�A���l(f��)��50min�ų�����|܇����|܇��ƽ���ٶȞ�180m/min���O(sh��)С�A���l(f��)x��min�����ߵ�·�̞�y��m�����D�е��۾���ʾС�A�����������^����y��m���cx��min��֮�g�ĺ���(sh��)�P(gu��n)ϵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
 ��D��Rt��ABC�У���ACB=90�㣬AC=6cm��BC=8cm�����cP���cB���l(f��)����BA߅����ÿ��5cm���ٶ����cA�����\�ӣ�ͬ�r���cQ���cC���l(f��)����CB߅����ÿ��4cm���ٶ����cB�����\�ӣ��\�ӕr�g��t�루0��t��2�����B��PQ��
��D��Rt��ABC�У���ACB=90�㣬AC=6cm��BC=8cm�����cP���cB���l(f��)����BA߅����ÿ��5cm���ٶ����cA�����\�ӣ�ͬ�r���cQ���cC���l(f��)����CB߅����ÿ��4cm���ٶ����cB�����\�ӣ��\�ӕr�g��t�루0��t��2�����B��PQ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com