
分析 (1)根據一元二次方程根與系數的關系及完全平方公式,即可求出sinA的值;
(2)根據根的判別式首先求出k的值,然后分兩種情況:①∠A是底角;②∠A是頂角,分別求出△ABC的第三邊的長度.
解答 解:(1)設關于x的方程9x2-9sinA•x-2=0的兩根為x1,x2,
則x1+x2=sinA,x1•x2=-$\frac{2}{9}$.
∴x12+x22=(x1+x2)2-2x1•x2=sin2A+$\frac{4}{9}$.
∵方程9x2-9sinA•x-2=0的兩根的平方和是1,
∴sin2A+$\frac{4}{9}$=1,
∴sinA=±$\frac{\sqrt{5}}{3}$,
∵∠A為銳角,
∴sinA=$\frac{\sqrt{5}}{3}$;
(2)依題意,知m、n是方程y2-6y+k2+4k+13=0的兩根,
則△≥0,
∴36-4(k2+4k+13)≥0,
∴-(k+2)2≥0,
∴(k+2)2≤0,
又∵(k+2)2≥0,
∴k=-2.
把k=-2代入方程,得y2-6y+9=0,
解得y=3,
∴m=n=3,
∴△ABC是等腰三角形.
分兩種情況:①∠A是底角;②∠A是頂角.
①當∠A是底角時,如圖,△ABC中,AB=BC=3,作底邊AB上的高BD,則AB=2AD.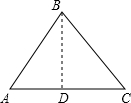 在直角△ABD中,
在直角△ABD中,
∵sinA=$\frac{\sqrt{5}}{3}$,
∴$\frac{BD}{AB}$=$\frac{\sqrt{5}}{3}$,
∴BD=$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2,
∴AC=4;
②當∠A是頂角時,如圖,△ABC中,AB=AC=3,作腰AC上的高BD. 在直角△ABD中,∵sinA=$\frac{\sqrt{5}}{3}$,
在直角△ABD中,∵sinA=$\frac{\sqrt{5}}{3}$,
∴$\frac{BD}{AB}$=$\frac{\sqrt{5}}{3}$,
∴BD=$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2,
∴CD=AC-AD=1.
在直角△ABD中,∵∠BDC=90°,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{6}$.
綜上可知,△ABC的第三邊的長度為4或$\sqrt{6}$.
點評 本題主要考查了根的判別式,根與系數的關系,等腰三角形的性質,三角函數的定義,綜合性強,難度較大.


科目:初中數學 來源: 題型:選擇題
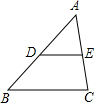 如圖,在△ABC中,點D、E分別是AB、AC的中點,則下列結論:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面積}{四邊形BCED的面積}=\frac{1}{3}$,其中正確的有( )
如圖,在△ABC中,點D、E分別是AB、AC的中點,則下列結論:①BC=3DE;②△ADE∽△ABC;$③\frac{AD}{AE}=\frac{AB}{AC}$;④$\frac{三角形ADE面積}{四邊形BCED的面積}=\frac{1}{3}$,其中正確的有( )| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 把一個斜邊長為10cm的含45°角的直角三角板放在三條互相平行的直線a,b,c,且直線a,b的距離和直線b,c之間的距離都是d,求d的值.
把一個斜邊長為10cm的含45°角的直角三角板放在三條互相平行的直線a,b,c,且直線a,b的距離和直線b,c之間的距離都是d,求d的值.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
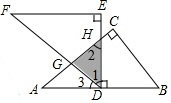 如圖所示,將兩塊全等的直角三角形紙片△ABC和△DEF疊放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,頂點D與邊AB的中點重合,DE⊥AB交AC于點H,DF交AC于點G,則重疊部分(△DGH)的面積為$\frac{75}{16}$.
如圖所示,將兩塊全等的直角三角形紙片△ABC和△DEF疊放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,頂點D與邊AB的中點重合,DE⊥AB交AC于點H,DF交AC于點G,則重疊部分(△DGH)的面積為$\frac{75}{16}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 所有有理數都有算術平方根 | B. | 一個數的算術平方根總是正數 | ||
| C. | 當a<0時,$\sqrt{a}$沒有意義 | D. | $\sqrt{a}$可以是正數,也可以是負數 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
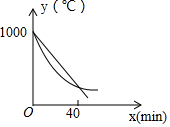 某研究所將某種材料加熱到1000℃時停止加熱,并立即將材料分為A、B兩組,采用不同工藝做降溫對比實驗,設降溫開始后經過xmin時,A、B兩組材料的溫度分別為yA℃、yB℃;yA、yB與x的函數關系式分別為yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分圖象如圖所示,當x=40時,兩組材料的溫度相同).
某研究所將某種材料加熱到1000℃時停止加熱,并立即將材料分為A、B兩組,采用不同工藝做降溫對比實驗,設降溫開始后經過xmin時,A、B兩組材料的溫度分別為yA℃、yB℃;yA、yB與x的函數關系式分別為yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分圖象如圖所示,當x=40時,兩組材料的溫度相同).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
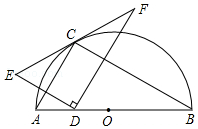 如圖,點C在以AB為直徑的半圓上,AB=8,∠CBA=30°,點D在線段AB上運動,點E與點D關于AC對稱,DF⊥DE于點D,并交EC的延長線于點F.下列結論:( )
如圖,點C在以AB為直徑的半圓上,AB=8,∠CBA=30°,點D在線段AB上運動,點E與點D關于AC對稱,DF⊥DE于點D,并交EC的延長線于點F.下列結論:( )| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com