
 把一個斜邊長為10cm的含45°角的直角三角板放在三條互相平行的直線a,b,c,且直線a,b的距離和直線b,c之間的距離都是d,求d的值.
把一個斜邊長為10cm的含45°角的直角三角板放在三條互相平行的直線a,b,c,且直線a,b的距離和直線b,c之間的距離都是d,求d的值. 分析 如圖,作AM⊥c于M,BN⊥c于N.先證明△ACM≌△BCN,推出AM=CN=d,CM=BM=2d,在等腰Rt△ABC中,由AB=10,推出AC=BC=5$\sqrt{2}$
在Rt△ACM中,根據AC2=AM2+CM2,可得d2+4d2=50,解方程即可.
解答 解:如圖,作AM⊥c于M,BN⊥c于N.
∵∠AMC=∠BNC=∠ACB=90°,
∴∠ACM+∠BCN=90°,∠BCN+∠CBN=90°,
∴∠ACM=∠CBN,
在△ACM和△CBN中,
$\left\{\begin{array}{l}{∠ACM=∠CBN}\\{∠AMC=∠BNC}\\{AC=CB}\end{array}\right.$,
∴△ACM≌△BCN,
∴AM=CN=d,CM=BM=2d,
在Rt△ABC中,∵AB=10,
∴AC=BC=5$\sqrt{2}$
在Rt△ACM中,∵AC2=AM2+CM2,
∴d2+4d2=50,
∴d=$\sqrt{10}$或-$\sqrt{10}$(舍棄),
∴d=$\sqrt{10}$.
點評 本題考查全等三角形的判定和性質、等腰直角三角形的性質,勾股定理等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
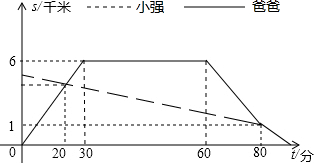 小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.
小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
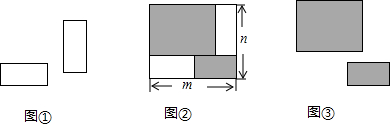
| A. | 4m | B. | 2(m+n) | C. | 4n | D. | 4(m-n) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
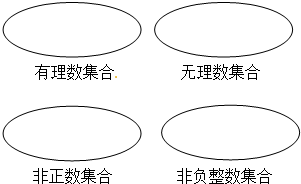
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com