
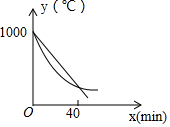
 某研究所將某種材料加熱到1000℃時停止加熱,并立即將材料分為A、B兩組,采用不同工藝做降溫對比實驗,設降溫開始后經過xmin時,A、B兩組材料的溫度分別為yA℃、yB℃;yA、yB與x的函數關系式分別為yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分圖象如圖所示,當x=40時,兩組材料的溫度相同).
某研究所將某種材料加熱到1000℃時停止加熱,并立即將材料分為A、B兩組,采用不同工藝做降溫對比實驗,設降溫開始后經過xmin時,A、B兩組材料的溫度分別為yA℃、yB℃;yA、yB與x的函數關系式分別為yA=kx+b,yB=$\frac{1}{4}$(x-60)2+m(部分圖象如圖所示,當x=40時,兩組材料的溫度相同).分析 (1)根據題意和函數圖象中的數據可以分別求得yA、yB與x的函數關系式;
(2)將y=120代入(1)中yA與x的函數關系式,然后將此時x的值再代入(1)中yB與x的函數關系式,本題得以解決;
(3)根據題意,將(1)中兩個函數解析式作差,然后根據0<x<40,即可解答本題.
解答 解:(1)由函數圖象可得,
當x=0時,yB=1000,
即1000=$\frac{1}{4}$(0-60)2+m,得m=100,
∴yB=$\frac{1}{4}$(x-60)2+100,
當x=40時,yB=$\frac{1}{4}$(40-60)2+100=200,
∴yA=kx+b過點(0,1000),(40,200),
∴$\left\{\begin{array}{l}{b=1000}\\{40k+b=200}\end{array}\right.$,得$\left\{\begin{array}{l}{k=-20}\\{b=1000}\end{array}\right.$,
∴yA=-20x+1000,
即yA與x的函數關系式為yA=-20x+1000,yB與x的函數關系式為yB=$\frac{1}{4}$(x-60)2+100;
(2)將yA=120代入yA=-20x+1000得,
120=-20x+1000,得x=44,
將x=44代入yB=$\frac{1}{4}$(x-60)2+100,得
yB=$\frac{1}{4}$(44-60)2+100=164,
即當A組材料的溫度降至120℃時,B組材料的溫度是164℃;
(3)由題意可得,
當0<x<40時,yA-yB=-20x+1000-$\frac{1}{4}$(x-60)2-100=-$\frac{1}{4}$x2+10x=-$\frac{1}{4}$(x-20)2+100,
∴當x=20時,兩組材料的溫差最大,此時兩組材料的溫差最大為100℃.
點評 本題考查二次函數的應用,解答此類問題的關鍵是明確題意,利用數形結合的思想和函數的思想解答本題.


 口算能手系列答案
口算能手系列答案科目:初中數學 來源: 題型:解答題
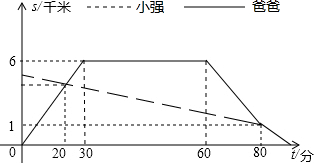 小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.
小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com