
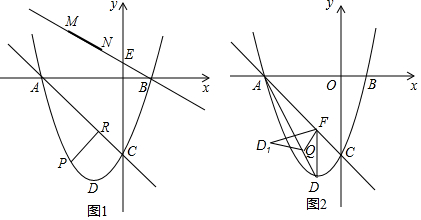
分析 (1)分別令x=0,y=0,可得A、B、C三點坐標,利用待定系數法設直線AC的解析式為y=kx+b,轉化為解方程組即可.
(2)如圖1中,設P(m,m2+2m-3),由題意,當PR最大時,△ACP的面積最大,即四邊形APCO的面積最大,因為S四邊形APCO=S△AOP+S△POC-S△AOC=$\frac{1}{2}$•3•(-m2-2m+3)+$\frac{1}{2}$•3•(-m)-$\frac{1}{2}$•3•3=-$\frac{3}{2}$m2-$\frac{9}{2}$m=-$\frac{3}{2}$(m+$\frac{3}{2}$)2+$\frac{27}{8}$,所以當m=-$\frac{3}{2}$時,四邊形APCO的面積最大,即PR最長,可得P(-$\frac{3}{2}$,-$\frac{15}{4}$),將點P沿BE方向平移$\sqrt{5}$個單位得到G(-$\frac{7}{2}$,-$\frac{11}{4}$),作點A關于直線BE的對稱點K,連接GK交BE于M,此時四邊形APNM的最長最小,想辦法求出點M的坐標即可解決問題.
(3)分三種情形討論即可①如圖2中,當FD1⊥AD時,重疊部分是Rt△FKQ.②如圖3中,當FQ⊥AD時,重疊部分是Rt△FQD1,③如圖4中,當QD1⊥AC時,重疊部分是Rt△QMF.分別求出AQ即可.
解答 解:(1)對于拋物線y=x2+2x-3,令y=0,得x2+2x-3=0,解得x=-3或1,
∴A(-3,0),B(1,0),
令x=0,得y=-3,
∴C(0,-3),
∵拋物線y=x2+2x-3=(x+1)2-4,
∴頂點D坐標為(-1,-4),
設直線AC的解析式為y=kx+b,則有$\left\{\begin{array}{l}{b=-3}\\{-3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
∴直線AC的解析式為y=-x-3,點D坐標(-1,-4).
(2)如圖1中,設P(m,m2+2m-3),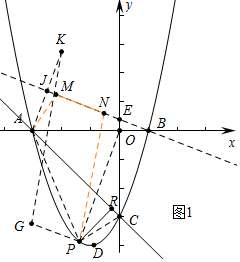
由題意,當PR最大時,△ACP的面積最大,即四邊形APCO的面積最大,
∵S四邊形APCO=S△AOP+S△POC-S△AOC=$\frac{1}{2}$•3•(-m2-2m+3)+$\frac{1}{2}$•3•(-m)-$\frac{1}{2}$•3•3=-$\frac{3}{2}$m2-$\frac{9}{2}$m=-$\frac{3}{2}$(m+$\frac{3}{2}$)2+$\frac{27}{8}$,
∴當m=-$\frac{3}{2}$時,四邊形APCO的面積最大,即PR最長,
∴P(-$\frac{3}{2}$,-$\frac{15}{4}$),
將點P沿BE方向平移$\sqrt{5}$個單位得到G(-$\frac{7}{2}$,-$\frac{11}{4}$),作點A關于直線BE的對稱點K,連接GK交BE于M,此時四邊形APNM的最長最小,
∵直線BE的解析式為y=-$\frac{1}{2}$x+$\frac{1}{2}$,直線AK的解析式為y=2x+6,
由$\left\{\begin{array}{l}{y=2x+6}\\{y=-\frac{1}{2}x+\frac{1}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{11}{5}}\\{y=\frac{8}{5}}\end{array}\right.$,
∴J(-$\frac{11}{5}$,$\frac{8}{5}$),
∵AJ=JK,
∴k(-$\frac{7}{5}$,$\frac{16}{5}$),
∴直線KG的解析式為y=$\frac{17}{6}$x+$\frac{43}{6}$,
由$\left\{\begin{array}{l}{y=\frac{17}{6}x+\frac{43}{6}}\\{y=-\frac{1}{2}x+\frac{1}{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=\frac{3}{2}}\end{array}\right.$,
∴M(-2,$\frac{3}{2}$),將點M向下平移1個單位,向右平移2個單位得到N,
∴N(0,$\frac{1}{2}$).
(3)存在.
①如圖2中,當FD1⊥AD時,重疊部分是Rt△FKQ,作QM⊥DF于M.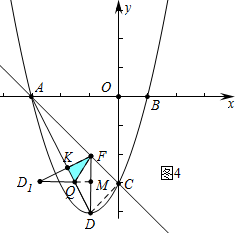
由題意可知F(-1,-2),DF=2,AF=2$\sqrt{2}$,AC=3$\sqrt{2}$,AD=2$\sqrt{5}$
由△AKF∽△ACD,得$\frac{AF}{AD}$=$\frac{FK}{CD}$=$\frac{AK}{AC}$,
∴$\frac{2\sqrt{2}}{2\sqrt{5}}$=$\frac{FK}{\sqrt{2}}$=$\frac{AK}{3\sqrt{2}}$
∴FK=$\frac{2\sqrt{5}}{5}$,AK=$\frac{6\sqrt{5}}{5}$,
∴DK=$\sqrt{{2}^{2}-(\frac{2\sqrt{5}}{5})^{2}}$=$\frac{4\sqrt{5}}{5}$,設QK=QM=x,
在Rt△QMD中,x2+(2-$\frac{2\sqrt{5}}{5}$)2=($\frac{4\sqrt{5}}{5}$-x)2,
∴x=1-$\frac{\sqrt{5}}{5}$,
∴AQ=AK+KQ=1+$\sqrt{5}$
②如圖3中,當FQ⊥AD時,重疊部分是Rt△FQD1,此時AQ=$\frac{6\sqrt{5}}{5}$.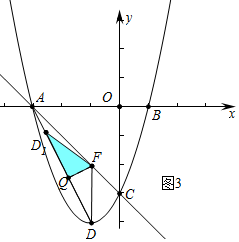
③如圖4中,當QD1⊥AC時,重疊部分是Rt△QMF.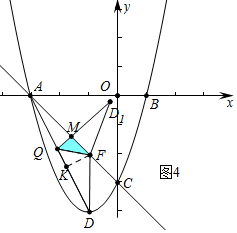
設QM=QK=x,在Rt△AQM中,x2+(2$\sqrt{2}$-$\frac{2\sqrt{5}}{5}$)2=($\frac{6\sqrt{5}}{5}$-x)2,
∴x=$\frac{2\sqrt{2}}{3}$-$\frac{2\sqrt{5}}{15}$,
∴AQ=AK-QK=$\frac{6\sqrt{5}}{5}$-($\frac{2\sqrt{2}}{3}$-$\frac{2\sqrt{5}}{15}$)=$\frac{4\sqrt{5}}{3}$-$\frac{2\sqrt{2}}{3}$.
綜上所述,當△D1FQ與△AFQ重疊部分的圖形是直角三角形時,AQ的長為1+$\sqrt{5}$或$\frac{6\sqrt{5}}{5}$或$\frac{4\sqrt{5}}{3}$-$\frac{2\sqrt{2}}{3}$.
點評 本題考查二次函數綜合題、一次函數的應用、直角三角形的性質、最短問題、二元一次方程組、勾股定理等知識,解題的關鍵是學會構建一次函數利用方程組求交點坐標,學會構建二次函數解決最值問題,學會利用對稱解決最短問題,學會用分類討論的思想思考問題,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
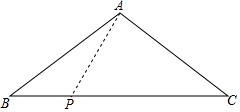 如圖,等腰三角形ABC的底邊長為8cm,腰長為5cm,一動點P在底邊上從點B向點C以1cm/s的速度移動,
如圖,等腰三角形ABC的底邊長為8cm,腰長為5cm,一動點P在底邊上從點B向點C以1cm/s的速度移動,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
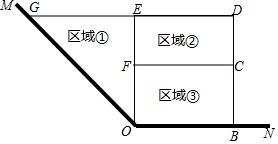 為了節省材料,某水產養殖戶利用水庫的一角∠MON(∠MON=135°)的兩邊為邊,用總長為120m的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形OBDG為直角梯形.
為了節省材料,某水產養殖戶利用水庫的一角∠MON(∠MON=135°)的兩邊為邊,用總長為120m的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形OBDG為直角梯形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,∠B、∠C的平分線相交于F,過點F作DE∥BC,交AB于D,交AC于E,那么下列結論:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周長為AB+AC;④BD=CE.其中正確的是( )
如圖,∠B、∠C的平分線相交于F,過點F作DE∥BC,交AB于D,交AC于E,那么下列結論:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周長為AB+AC;④BD=CE.其中正確的是( )| A. | ③④ | B. | ①② | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
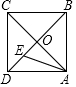 如圖,正方形ABCD的邊長為a,AC與BD交于點O,E為OD中點,動點P從點O出發,沿折O→E→A→B→O的路徑運動,回到點O時運動停止.設點P運動的路程長為x,AP長為y,則y關于x的函數圖象大致是 ( )
如圖,正方形ABCD的邊長為a,AC與BD交于點O,E為OD中點,動點P從點O出發,沿折O→E→A→B→O的路徑運動,回到點O時運動停止.設點P運動的路程長為x,AP長為y,則y關于x的函數圖象大致是 ( )| A. | 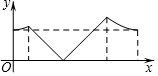 | B. | 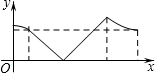 | ||
| C. | 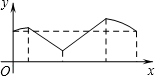 | D. | 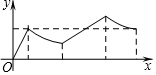 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com