
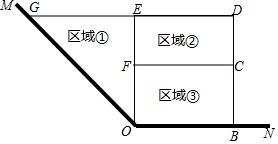
 為了節省材料,某水產養殖戶利用水庫的一角∠MON(∠MON=135°)的兩邊為邊,用總長為120m的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形OBDG為直角梯形.
為了節省材料,某水產養殖戶利用水庫的一角∠MON(∠MON=135°)的兩邊為邊,用總長為120m的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形OBDG為直角梯形.分析 (1)首先證明EG=EO=DB,DE=FC=OB,設OB=CF=DE=x,則GE=OE=BD=$\frac{1}{3}$(120-3x)=40-x,由①②③這塊區域的面積相等,得到$\frac{1}{2}$(40-x)2=$\frac{1}{2}$•x(40-x),解方程即可.
(2)①根據直角梯形的面積公式計算即可.②由S1:S2:S3=3:2:1,肯定$\frac{1}{2}$(40-x)2=$\frac{1}{2}$(-$\frac{1}{2}$x2+800),推出x=$\frac{40}{3}$或40(舍棄),求得EG=40-$\frac{40}{3}$=$\frac{80}{3}$,ED=$\frac{40}{3}$,DC=$\frac{2}{3}$EG=$\frac{160}{9}$,由此即可解決問題.
解答 解:(1)由題意可知,∠MON=135°,∠EOB=∠D=∠DBO=90°,
∴∠EGO=∠EOG=45°,
∴EG=EO=DB,DE=FC=OB,設OB=CF=DE=x,則GE=OE=BD=$\frac{1}{3}$(120-3x)=40-x,
∵①②③這塊區域的面積相等,
∴$\frac{1}{2}$(40-x)2=$\frac{1}{2}$•x(40-x),
∴x=20或40(舍棄),
∴BC=20m.
故答案為20.
(2)①y=$\frac{x+x+40-x}{2}$•(40-x)=-$\frac{1}{2}$x2+800(0<x<40).
②∵S1:S2:S3=3:2:1,
∴$\frac{1}{2}$(40-x)2=$\frac{1}{2}$(-$\frac{1}{2}$x2+800),
∴x=$\frac{40}{3}$或40(舍棄),
∴EG=40-$\frac{40}{3}$=$\frac{80}{3}$,ED=$\frac{40}{3}$,DC=$\frac{2}{3}$EG=$\frac{160}{9}$,
∴EG:DE:DC=$\frac{80}{3}$:$\frac{40}{3}$:$\frac{160}{9}$=6:3:4.
點評 本題考查一元二次方程的應用、三角形的面積公式、矩形的性質、直角梯形的性質等知識,解題的關鍵是學會利用參數構建方程解決問題,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
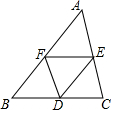 如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 各有一個角是45°的兩個等腰三角形 | |
| B. | 兩個等邊三角形 | |
| C. | 各有一個角是45°,腰長都是3cm的兩個等腰三角形 | |
| D. | 腰和頂角對應相等的兩個等腰三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a-3b2÷a-2b2=$\frac{1}{a}$ | B. | (-$\frac{3x}{4y}$)4=-$\frac{3{x}^{4}}{-4{y}^{3}}$ | ||
| C. | ($\frac{2a}{a+c}$)2=$\frac{{a}^{2}}{{c}^{2}}$ | D. | $\frac{b}{a}$+$\fracp9vv5xb5{c}$=$\frac{bd}{ac}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com